
分析 (Ⅰ)把曲线C的极坐标方程、直线l的参数方程化为普通方程,由曲线C与直线l一个交点的横坐标求出对应的纵坐标,即可求出a的值以及曲线C的普通方程,再化普通方程为参数方程即可;
(Ⅱ)由曲线C表示圆,求出圆心到直线的距离,利用勾股定理求出对应的弦长.
解答 解:(Ⅰ)曲线C的极坐标方程ρ=acosθ可化为ρ2=aρcosθ,
化为一般方程是x2+y2=ax,
直线l的参数方程$\left\{{\begin{array}{l}{x=\frac{{\sqrt{2}}}{2}t+2}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.(t为参数)$,
消去参数t,得x-y=2;
又曲线C与直线l一个交点的横坐标为3-$\sqrt{7}$,
∴对应的纵坐标为y=x-2=1-$\sqrt{7}$;
∴a=$\frac{{x}^{2}{+y}^{2}}{x}$=x+$\frac{{y}^{2}}{x}$=(3-$\sqrt{7}$)+$\frac{{(1-\sqrt{7})}^{2}}{3-\sqrt{7}}$=(3-$\sqrt{7}$)+(5+$\sqrt{7}$)=8;
∴曲线C的一般方程为x2+y2=8x,
即(x-4)2+y2=16;
又设$\frac{x-4}{4}$=cosα,$\frac{y}{4}$=sinα,
∴x=4+4cosα,y=4sinα;
即曲线C的参数方程为$\left\{\begin{array}{l}{x=4+4cosα}\\{y=4sinα}\end{array}\right.$(α为参数);…(3分)
(Ⅱ)∵曲线C表示圆C,且圆C的圆心为(4,0),
圆心到直线的距离为$d=\sqrt{2}$,
∴所求的弦长为
2$\sqrt{{r}^{2}{-d}^{2}}$=$2\sqrt{{4^2}-{{({\sqrt{2}})}^2}}=2\sqrt{14}$.(7分)
点评 本题考查了直线与圆的方程的应用问题,也考查了参数方程与极坐标方程的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,0) | C. | (0,1] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2014}$ | B. | $\frac{1}{{2}^{2014}}$ | C. | $\frac{1}{2015}$ | D. | $\frac{1}{{2}^{2015}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
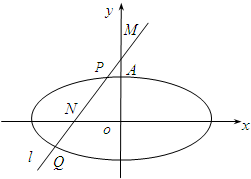 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于P,Q不同两点,点N在线段PQ上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{{\sqrt{2}}}{2}$ | C. | xy=±2$\sqrt{2}$x | D. | y=±$\sqrt{11}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com