
分析 (1)利用绝对值不等式的解法求解可得M,然后利用作差法证明不等式即可.
(2)判断三个数都是正数,然后求解3个数的乘积,推出h的范围,即可得到结果.
解答 解 (1)不等式|2x-1|<1,可得-1<2x-1<1,即0<x<1,所以不等式的解集为:M={x|0<x<1},
∵a,b∈M,
∴ab+1-a-b=(a-1)(b-1)>0,
∴ab+1>a+b…..(6分)
(2)设max{A}表示数集A中的最大数,且$h=max\{\frac{2}{{\sqrt{a}}},\frac{a+b}{{\sqrt{ab}}},\frac{ab+1}{{\sqrt{b}}}\}$,∵$h≥\frac{2}{{\sqrt{a}}},h≥\frac{a+b}{{\sqrt{ab}}},h≥\frac{ab+1}{{\sqrt{b}}}$,3个数都是正数,
∴${h^3}≥\frac{2(a+b)(ab+1)}{ab}$
由(1)ab+1>a+b
∴${h^3}>\frac{{2{{(a+b)}^2}}}{ab}≥\frac{{2{{(2\sqrt{ab})}^2}}}{ab}=8$,
h>2…..(12分)
$或∵ab+1≥2\sqrt{ab},a+b≥2\sqrt{ab}(当且仅当a=b=1时取等号)$,
∴${h^3}≥\frac{2(a+b)(ab+1)}{ab}>\frac{{8{{(\sqrt{ab})}^2}}}{ab}=8$
(∵0<a<1,0<b<1,∴等号取不到)
∴h>2.
点评 本题考查不等式的证明,绝对值不等式的解法,函数的最值的应用,考查计算能力.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,-$\sqrt{3}$]∪[$\sqrt{3}$,2) | B. | [-2,-$\sqrt{3}$)∪($\sqrt{3}$,2] | C. | [-2,2] | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
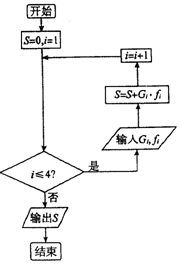 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:| 序号 (i) | 分组 (分数) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [60,70) | 65 | ① | 0.10 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.20 |
| 4 | [90,100) | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}-π-cos2$ | B. | $\frac{11}{6}-π+\frac{1}{2}cos2$ | C. | $\frac{17}{6}-π-\frac{1}{2}cos2$ | D. | $\frac{11}{6}-π-\frac{1}{2}cos2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com