
 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,分析 ( 1)根据面面垂直的判定定理推断出平面ADE⊥平面BCE;
(2)由BD交平面ACE的交点为BD的中点,可是点D与点B到平面ACE的距离相等,进而根据BF⊥平面ACE,所以BF为点B到平面ACE的距离,解三角形ABE和三角形CBE可得答案.
(3)在△ABE中过M点作MG∥AE交BE于G点,在△BEC中过G点作GN∥BC交EC于N点,连MN,证明平面MGE∥平面ADE,可得MN∥平面ADE,从而可得结论.
解答 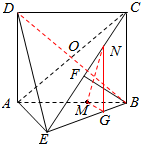 证明:(Ⅰ)∵BF⊥平面ACE,AE?平面ACE,
证明:(Ⅰ)∵BF⊥平面ACE,AE?平面ACE,
∴BF⊥AE,BF⊥CE,
∵EB=BC,∴F是CE的中点,
又∵AD⊥平面ABE,AD?平面ABCD,
∴平面ABCD⊥平面ABE,
∵平面ABCD∩平面ABE=AB,BC⊥AB
∴BC⊥平面ABE,
从而BC⊥AE,且BC∩BF=B,
∴AE⊥平面BCE,
又AE?平面ADE,
故平面平面ADE⊥平面BCE.
(2)(Ⅱ)如图,连接BD交AC于点O,则点O是BD的中点,
∴点D与点B到平面ACE的距离相等.
∵BF⊥平面ACE,
∴BF为点B到平面ACE的距离.
∵AE⊥平面BCE,∴AE⊥BE.
又∵AE=BE,
∴△AEB是等腰直角三角形,
∵AE=2,∴AB=2$\sqrt{2}$,∴BE=2$\sqrt{2}$sin45°=$2\sqrt{2}×\frac{\sqrt{2}}{2}$=2,
又在Rt△CBE中,CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=2$\sqrt{2}$,
∴BF=$\frac{BC×BE}{CE}$=$\frac{2×2}{2\sqrt{2}}$=$\sqrt{2}$.
故点D到平面ACE的距离是$\sqrt{2}$.
(3)在△ABE中过M点作MG∥AE交BE于G点,
在△BEC中过G点作GN∥BC交EC于N点,连MN,
∴CN=$\frac{1}{3}$CE.
∵MG∥AE,MG?平面ADE,AE?平面ADE,
∴MG∥平面ADE.
同理,GN∥平面ADE,且MG与GN交于G点,
∴平面MGE∥平面ADE.
又MN?平面MGN,
∴MN∥平面ADE.
故N点为线段CE上靠近C点的一个三等分点.
点评 本题考查面面垂直和线面平行的判定,以及点到平面的距离的计算,考查了推理论证和逻辑思维能力.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{80}{3}$ | B. | $\frac{255}{4}$ | C. | $\frac{624}{5}$ | D. | $\frac{1295}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是边AA1,CC1的中点,点M是BB1上的动点,过点E,M,F的平面与棱DD1交于点N,设BM=x,平行四边形EMFN的面积为S,设y=S2,则y关于x的函数y=f(x)的解析式为( )
已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是边AA1,CC1的中点,点M是BB1上的动点,过点E,M,F的平面与棱DD1交于点N,设BM=x,平行四边形EMFN的面积为S,设y=S2,则y关于x的函数y=f(x)的解析式为( )| A. | $f(x)=2{x^2}-2x+\frac{3}{2}$,x∈[0,1] | |
| B. | $f(x)=\left\{\begin{array}{l}\frac{3}{2}-x,x∈[0\;,\;\frac{1}{2})\\ x+\frac{1}{2},x∈[\frac{1}{2}\;,\;1].\end{array}\right.$ | |
| C. | $f(x)=\left\{\begin{array}{l}-2{x^2}+\frac{3}{2},x∈[0\;,\;\frac{1}{2}]\\-2{(x-1)^2}+\frac{3}{2},x∈(\frac{1}{2}\;,\;1].\end{array}\right.$ | |
| D. | $f(x)=-2{x^2}+2x+\frac{3}{2}$,x∈[0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
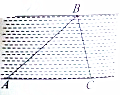 如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,现在岸边取基线AC,测得AC=120m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.
如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,现在岸边取基线AC,测得AC=120m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com