考点:平面与平面垂直的判定,直线与平面所成的角
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(Ⅰ)通过计算证得CE⊥DE,再由D1D⊥CE,则CE⊥面D1DE,由面面垂直的判定定理,即可得证;
(Ⅱ)过B作BH⊥面CED1,垂足为H,连接CH,则∠BCH为直线BC与平面CD1E所成角.由VB-CD1E=VD1-BCE,可求出高BH,即可求出所成角的正弦.
解答:
(Ⅰ)证明:在矩形ABCD中,E为AB的中点,AD=2,AB=4,
∴DE=CE=2
,
∵CD=4,∴CE⊥DE,
∵D
1D⊥面ABCD,∴D
1D⊥CE,
∴CE⊥面D
1DE,
又CE?面CED
1,
∴平面DD
1E⊥平面CD
1E;
(Ⅱ)过B作BH⊥面CED
1,垂足为H,连接CH,
则∠BCH为直线BC与平面CD
1E所成角.
∵CE⊥面D
1DE,∴CE⊥D
1E,
在直角△D
1DE中,D
1E=2
,
由V
B-CD1E=V
D1-BCE,
则
S
△CD1E•BH=
S
△BCE•D
1D,
即
×
2×2
•BH=
×4×2,解得BH=
,
故直线BC与平面CD
1E所成角的正弦值为
=
.
点评:本题考查直线与平面垂直的判定和性质、平面与平面垂直的判定定理,考查直线与平面所成的角,考查等积法,求三棱锥的高,考查运算能力,属于中档题.

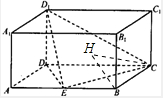
 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点. (Ⅰ)证明:在矩形ABCD中,E为AB的中点,AD=2,AB=4,
(Ⅰ)证明:在矩形ABCD中,E为AB的中点,AD=2,AB=4,

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案