
| AЃЎ | {6ЃЌ$\frac{5}{4}$} | BЃЎ | {6ЃЌ$\frac{5}{4}$ЃЌ$\frac{2}{5}$} | CЃЎ | {6ЃЌ$\frac{5}{4}$ЃЌ$\frac{1}{5}$} | DЃЎ | {6ЃЌ$\frac{1}{5}$} |
ЗжЮі ЖдmЗжРрЬжТлЃЌРћгУЕнЭЦЙиЯЕМДПЩЕУГіЃЎ
НтД№ НтЃКЪ§Са{an}Тњзуa1=mЃЈmЃО0ЃЉЃЌ${a}_{n+1}=\left\{\begin{array}{l}{{a}_{n}-1ЃЌ{a}_{n}ЃО1}\\{\frac{1}{{a}_{n}}ЃЌ0ЃМ{a}_{n}Ём1}\end{array}\right.$ЃЌa3=4ЃЌ
ЂйШєmЃО2ЃЌдђa2=m-1ЃО1ЃЌЁрa3=m-2=4ЃЌНтЕУm=6ЃЎ
ЂкШєm=2ЃЌдђa2=m-1=1ЃЌЁрa3=$\frac{1}{{a}_{2}}$=1Ёй4ЃЌЩсШЅЃЎ
ЂлШє1ЃМmЃМ2ЃЌдђa2=m-1ЁЪЃЈ0ЃЌ1ЃЉЃЌЁрa3=$\frac{1}{m-1}$=4ЃЌНтЕУm=$\frac{5}{4}$ЃЎ
ЂмШєm=1ЃЌдђa2=$\frac{1}{{a}_{1}}$=1ЃЌЁрa3=$\frac{1}{{a}_{2}}$Ёй4ЃЌЩсШЅЃЎ
ЂнШє0ЃМmЃМ1ЃЌдђa2=$\frac{1}{{a}_{1}}$=$\frac{1}{m}$ЃО1ЃЌЁрa3=a2-1=$\frac{1}{m}$-1=4ЃЌНтЕУm=$\frac{1}{5}$ЃЎ
злЩЯПЩЕУЃКmЁЪ$\{6ЃЌ\frac{5}{4}ЃЌ\frac{1}{5}\}$ЃЎ
ЙЪбЁЃКCЃЎ
ЕуЦР БОЬтПМВщСЫЕШБШЪ§СаЕФЭЈЯюЙЋЪНЁЂЕнЭЦЙиЯЕЃЌПМВщСЫЗжРрЬжТлЗНЗЈЁЂЭЦРэФмСІгыМЦЫуФмСІЃЌЪєгкжаЕЕЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЃЈ1ЃЌ+ЁоЃЉ | BЃЎ | [$\frac{\sqrt{10}}{2}$ЃЌ+ЁоЃЉ | CЃЎ | ЃЈ1ЃЌ$\frac{\sqrt{10}}{2}$] | DЃЎ | ЃЈ1ЃЌ$\frac{5}{2}$] |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЃЈ-ЁоЃЌ1] | BЃЎ | ЃЈ-ЁоЃЌe${\;}^{\frac{Іа}{2}}$] | CЃЎ | ЃЈ1ЃЌe${\;}^{\frac{Іа}{2}}$ЃЉ | DЃЎ | [e${\;}^{\frac{Іа}{2}}$ЃЌ+ЁоЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | cЃОbЃОa | BЃЎ | bЃОcЃОa | CЃЎ | aЃОcЃОb | DЃЎ | aЃОbЃОc |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2016-2017бЇФъЩНЮїаУжнвЛжаИпвЛЩЯбЇЦкаТЩњУўЕзЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ЯШЛЏМђЃЌдйЧѓжЕЃК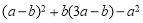 ЃЌЦфжа
ЃЌЦфжа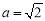 ЃЌ
ЃЌ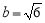 .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{1}{3}$ | BЃЎ | $\frac{\sqrt{3}-1}{2}$ | CЃЎ | $\frac{\sqrt{2}-1}{2}$ | DЃЎ | $\frac{\sqrt{3}}{4}$ |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com