考点:用空间向量求平面间的夹角,棱柱、棱锥、棱台的体积,与二面角有关的立体几何综合题
专题:空间向量及应用
分析:(Ⅰ)求出三棱锥P-ABC的底面积和高,即可求出三棱锥的体积;
(Ⅱ)根据二面角的定义或者利用向量法即可求二面角C-DA-E的平面角.
解答:

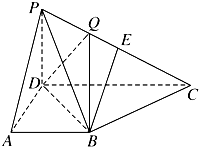
解:证明:(Ⅰ)取AC的中点O,连接OP,OB(图1),(1分)
易得:OP⊥0A,OP=
==…(2分)
∵AC=4,AB=2,BC=2
,
∴AC
2=AB
2+BC
2,
∴△ABC为直角三角形,
即OB=OC=2.
∴PB
2=OB
2+OP
2,即OP⊥OB.…(4分)
又∵AC∩BO=O,且AC,0B?面ABC,
∴OP⊥平面ABC…(5分)
三棱锥P-ABC的体积V=
•OP•AB•BC=3.…(6分)
(Ⅱ)法一:(图2)作EG⊥AC,GH⊥DF于G,H点,连接EH,
∵OP平面ABC,EG?平面ABC,EG⊥OP …(7分)
又AC∩OP=O,且AC,0P?面PAC,
∴EG⊥平面PAC.
∵DA?平面PAC,
∴DA⊥EG …(8分)
又EG∩GH=G,且EG,GH?面EGH,
∴DA⊥平面EGH…(9分)
∵EH?面EGH,
∴EH⊥DA…(10分)
∴∠EHG为二面角C-DF-E的平面角.…(11分)
∵EG=CEsin30°=
,CG=CEcos30
°=,AG=
,
由(Ⅰ)知OP=
,
∴AD=
==.
∴
S△DAG=×OP•AG=GH•DA,
∴GH=
,
∴tan
∠EHG=,
∴
∠EHG=…(14分)
法二:以O为原点,以OC,OP为y,z轴建系,则D(0,1,
),E(
,,0),A(0,-2,0),(8分)
设
=(1,y,z)为平面DEA的法向量,则有
| | •=(1,y,z)•(,-,-)=0 | | •=(1,y,z)•(0,-3,-)=0 |
| |
,
即
…(11分)
∴y=-
,z=
…(12分)
又∵
=(,0,0)为平面DEA的法向量,
∴
cos?θ===,
二面角C-DA-E的平面角为
.…(14分)
点评:本题主要考查空间几何体的体积计算,以及空间二面角的计算,综合考查学生的计算能力.

 在三棱锥P-ABC中,侧棱长均为
在三棱锥P-ABC中,侧棱长均为 解:证明:(Ⅰ)取AC的中点O,连接OP,OB(图1),(1分)
解:证明:(Ⅰ)取AC的中点O,连接OP,OB(图1),(1分)

 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,若 E为PC的中点,且BE与平面PDC所成的角的正弦值为
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,若 E为PC的中点,且BE与平面PDC所成的角的正弦值为 如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.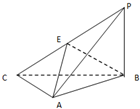 如图,三棱锥P-ABC中,PA⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC中点.
如图,三棱锥P-ABC中,PA⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC中点.