
| A. | (k-$\frac{1}{8}$,k+$\frac{1}{8}$),k∈Z | B. | (2k-$\frac{1}{8}$,2k+$\frac{1}{8}$),k∈Z | C. | (4k-$\frac{1}{8}$,4k+$\frac{1}{8}$),k∈Z | D. | (8k-$\frac{1}{8}$,8k+$\frac{1}{8}$),k∈Z |
分析 根据函数奇偶性的性质求出函数周期性和对称性,作出函数的图象,利用函数与方程的关系转化为两个函数的交点问题,求函数的导数,利用曲线相切的性质进行即可.
解答 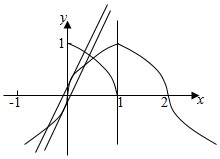 解:∵函数f(x)是定义在R上的奇函数,且f(x-1)为偶函数,
解:∵函数f(x)是定义在R上的奇函数,且f(x-1)为偶函数,
∴f(-x-1)=f(x-1)=-f(x+1),
则f(x)=-f(x+2),
则f(x+4)=f(x),则函数f(x)是周期为4的周期函数
且函数f(x-1)关于y轴对称,即函数f(x)关于x=-1对称,
若x∈[-1,0],则-x∈[0,1]时,此时f(-x)=(-x)${\;}^{\frac{1}{2}}$=$\sqrt{-x}$=-f(x),
则f(x)=-$\sqrt{-x}$,x∈[-1,0],
由g(x)=f(x)-2x-b有三个零点,
得g(x)=f(x)-2x-b=0,即f(x)=2x+b有三个根,
作出函数f(x)和y=2x+b的图象如图:
当y=2x+b与f(x)=x${\;}^{\frac{1}{2}}$在[0,1]内相切时,
得f′(x)=$\frac{1}{2\sqrt{x}}$,
由f′(x)=$\frac{1}{2\sqrt{x}}$=2得$\sqrt{x}$=$\frac{1}{4}$,即x=$\frac{1}{16}$,此时y=$\frac{1}{4}$,
即切点坐标为($\frac{1}{16}$,$\frac{1}{4}$),
此时由2×$\frac{1}{16}$+b=$\frac{1}{4}$得b=$\frac{1}{8}$,
当y=2x+b与f(x)=-$\sqrt{-x}$在[-1,0]内相切时,
得f′(x)=$\frac{1}{2\sqrt{-x}}$,
由f′(x)=$\frac{1}{2\sqrt{-x}}$=2得$\sqrt{-x}$=$\frac{1}{4}$,即-x=$\frac{1}{16}$,此时y=-$\frac{1}{4}$,
即切点坐标为(-$\frac{1}{16}$,-$\frac{1}{4}$),
此时由2×(-$\frac{1}{16}$)+b=-$\frac{1}{4}$得b=-$\frac{1}{8}$,此时两个函数有2个交点,
若g(x)=f(x)-2x-b有三个零点,
则-$\frac{1}{8}$<b<$\frac{1}{8}$,
∵函数的周期是4,
∴4k-$\frac{1}{8}$<b<4k+$\frac{1}{8}$,k∈Z,
故选:C
点评 本题主要考查函数零点个数的应用,综合考查函数与方程的转化,根据条件求出函数的周期性,利用函数周期性和奇偶性对称性的性质进行转化是解决本题的关键.综合性较强,难度较大.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
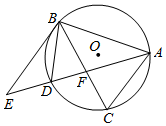 如图,△ABC内接于圆O,过B点的切线为BE,∠CBE的角平分线交圆O于点D,连接AD交BC于F,延长交BE于E.
如图,△ABC内接于圆O,过B点的切线为BE,∠CBE的角平分线交圆O于点D,连接AD交BC于F,延长交BE于E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2i | B. | -2i | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设椭圆$\frac{{x}^{2}}{4}$+y2=1的右顶点为A,过椭圆长轴所在直线上的一个定点M(m,0)(不同于A)任作一条直线与椭圆相交于P、Q两点,直线AP、AQ的斜率分别记为k1、k2.
设椭圆$\frac{{x}^{2}}{4}$+y2=1的右顶点为A,过椭圆长轴所在直线上的一个定点M(m,0)(不同于A)任作一条直线与椭圆相交于P、Q两点,直线AP、AQ的斜率分别记为k1、k2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-3,-1) | C. | (1,5) | D. | (-5,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com