练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    {an}的前n项和为Sn，若(a2－1)3＋2012(a2－1)＝1，(a2011－1)3＋2012·(a2011－1)＝－1，则下列四个命题中真命题的序号为________．

    ①S2011＝2011；②S2012＝2012；③a2011<a2；④S2011<S2.


    ②③

    [解析]　设f(x)＝x3＋2012x，则f(x)为奇函数，f ′(x)＝3x2＋2012>0，∴f(x)单调递增．由f(1)＝2013>1知f(1)>f(a2－1)，∴1>a2－1，∴a2<2.

    又f(a2－1)＝－f(a2011－1)＝f(1－a2011)，∴a2－1＝1－a2011，∴a2＋a2011＝2，∴S2012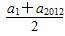＝×2012＝2012，故②正确；

    又f(a2－1)>f(a2011－1)，∴a2－1>a2011－1，

    ∴a2011<a2，∴③正确；

    S2011＝S2012－a2012＝2012－(a2011＋d)＝2012－(2－a2＋d)＝2010＋a1>a1＋a2＝S2，∴④错误；

    假设S2011＝2011，则2010＋a1＝2011，∴a1＝1，

    ∵S2011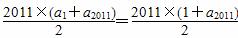＝＝2011，∴a2011＝1，这与{an}是等差数列矛盾，∴①错．

    综上，正确的为②③.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    直线ax＋by＋c＝0与圆x2＋y2＝9相交于两点M、N，若c2＝a2＋b2，则(O为坐标原点)等于(　　)

    A．－7  B．－14  C．7  D．14

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知整数对按如下规律排成一列：(1,1)，(1,2)，(2,1)，(1,3)，(2,2)，(3,1)，(1,4)，(2,3)，(3,2)，(4,1)，……则第2014个数对是(　　)

    A．(3,61)                                                      B．(3,60)

    C．(61,3)                                                      D．(61,2)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn表示等差数列{an}的前n项和，已知＝，那么等于(　　)

    A.  B.  C.  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}的公差d＝1，前n项和为Sn.

    (1)若1，a1，a3成等比数列，求a1；

    (2)若S5>a1a9，求a1的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的首项a1＝1，且满足an＋1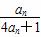＝ (n∈N*)．

    (1)设bn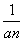＝，求证：数列{bn}是等差数列，并求数列{an}的通项公式；

    (2)设cn＝bn·2n，求数列{cn}的前n项和Sn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项的和Sn满足Sn＝2n－1(n∈N*)，则数列{a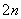}的前n项的和为(　　)

    A．4n－1                                                       B.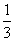(4n－1)

    C.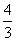(4n－1)                                                   D．(2n－1)2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某程序框图如图所示，该程序运行后输出的k的值是(　　)

    A．4  B．5  C．6  D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝a1x＋a2x2＋…＋anxn(n为正偶数)且{an}为等差数列，f(1)＝n2，f(－1)＝n，试比较与3的大小，并证明你的结论．

    查看答案和解析>>

    同步练习册答案