
分析 在100张卡片上分别写上1至100这100个数字,从中任取一张共有100种取法,其中所得卡片上的数字为6的倍数的数是6,12,…,96,可得出满足条件的数据的个数,再利用古典概型的概率计算公式即可得出.
解答 解:在100张卡片上分别写上1至100这100个数字,从中任取一张共有100种取法,
其中所得卡片上的数字为6的倍数的数是:
6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96共16个,
∴所得卡片上的数字为6的倍数的数共有16个.
∴所得卡片上的数字为6的倍数的概率P=$\frac{16}{100}$=$\frac{4}{25}$,
故答案为:$\frac{4}{25}$.
点评 本题考查了古典概型的概率计算公式和等差数列的通项公式,属于基础题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
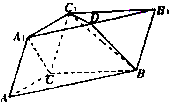 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
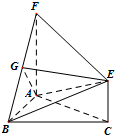 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
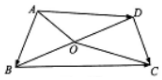 如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,则$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.
如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,则$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=-\sqrt{x^2}$ | B. | $y=\frac{-x(x-1)}{x-1}$ | ||
| C. | y=-logaax(a>0且a≠1) | D. | $y=-\sqrt{x}•\sqrt{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3] | B. | [-2$\sqrt{2}$,3] | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com