
 ���ݡ�2015����ú���ᷢչͳ�ƹ������й��������ݣ���2011 �굽2015 �꣬�ҹ��ĵ�����ҵ��GDP�еı������£�
���ݡ�2015����ú���ᷢչͳ�ƹ������й��������ݣ���2011 �굽2015 �꣬�ҹ��ĵ�����ҵ��GDP�еı������£�| ��� | 2011 | 2012 | 2013 | 2014 | 2015 |
| ��ݴ���x | 1 | 2 | 3 | 4 | 5 |
| ������ҵ���أ�%�� | 44.3 | 45.5 | 46.9 | 48.1 | 50.5 |
���� ��1����������������������㻭��ɢ��ͼ���ɣ�
��2����������������ĵ㣬Ȼ�����ûع鷽�̼��㹫ʽ��⼴�ɣ�
��3�����ûع鷽�̵�Ԥ�����ý�ϣ�2���еĽ������Ԥ�⼴�ɣ�
��� �⣺��1���������������ݻ���ɢ��ͼ��ͼ��ʾ��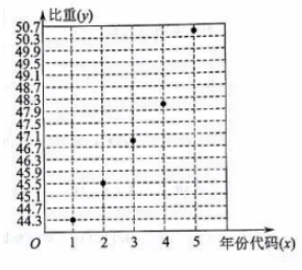
��2������������ݼ���ɵã�
$\overline{x}=\frac{1+2+3+4+5}{5}=3$��$\overline{y}=\frac{44.3+45.5+46.9+48.1+50.5}{5}=47.06$��
��$\widehat{b}=\frac{\sum_{i=1}^{n=5}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{5}{��{x}_{i}-\overline{x}��}^{2}}=1.5$��$\widehat{a}=\overline{y}-\widehat{b}\overline{x}=42.56$��
�ʻع鷽��Ϊ��$\widehat{y}=\widehat{b}x+\hat{a}=1.5x+42.56$��
��3������2017�����ݴ���x=7�ɵã�$\hat{y}=1.5��7+42.56=53.06$��
�ʰ��յ�ǰ�ı仯���ƣ�Ԥ��2017 ���ҹ�������ҵ��GDP�еı��ؽ��ﵽ53.06%��
���� ���⿼��ع鷽�̵Ķ��弰��Ӧ�ã�ɢ��ͼ�Ļ��Ƶȣ��ص㿼��ѧ���Ի������������ͼ��������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{2}$ | B�� | $-\frac{{\sqrt{3}}}{2}$ | C�� | $\frac{{\sqrt{3}}}{2}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �ڢ� | C�� | �ڢ� | D�� | �٢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 19 | C�� | 17 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��\frac{1}{2}��2]$ | B�� | [1��2] | C�� | ��1��2] | D�� | $��\frac{1}{2}��2��$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com