
(本题满分14分,第1小题6分,第2小题8分)
已知函数 ,其中常数a > 0.
,其中常数a > 0.
(1) 当a = 4时,证明函数f(x)在 上是减函数;
上是减函数;
(2) 求函数f(x)的最小值.
(1)任取0<x1<x2≤2,则f(x1)–f(x2)=
 ,
,
因为0<x1<x2≤2,所以f(x1)–f(x2)>0,即f(x1)>f(x2);
(2) 。
。
解析试题分析:(1) 当 时,
时, ,…………………………………………1分
,…………………………………………1分
任取0<x1<x2≤2,则f(x1)–f(x2)=
 ………………3分
………………3分
因为0<x1<x2≤2,所以f(x1)–f(x2)>0,即f(x1)>f(x2)………………………………………5分
所以函数f(x)在 上是减函数;………………………………………………………6分
上是减函数;………………………………………………………6分
(2)
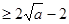 ,……………………………………………………7分
,……………………………………………………7分
当且仅当 时等号成立,…………………………………………………………8分
时等号成立,…………………………………………………………8分
当 ,即
,即 时,
时,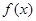 的最小值为
的最小值为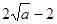 ,………………………10分
,………………………10分
当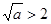 ,即
,即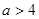 时,
时,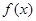 在
在 上单调递减,…………………………………11分
上单调递减,…………………………………11分
所以当 时,
时,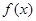 取得最小值为
取得最小值为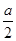 ,………………………………………………13分
,………………………………………………13分
综上所述: ………………………………………14分
………………………………………14分
考点:函数的单调性和最值;基本不等式。
点评:用定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
一片森林原来面积为 ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的 ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的 .
.
(Ⅰ)求每年砍伐面积的百分比;
(Ⅱ)到今年为止,该森林已砍伐了多少年?
(Ⅲ)今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若存在x0∈R,使方程
,若存在x0∈R,使方程 成立,则称x0为
成立,则称x0为 的不动点,已知函数
的不动点,已知函数 (a≠0).
(a≠0).
(1)当 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数b,函数 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com