Question

13．在△ABC中，若向量$\overrightarrow{BA}$，$\overrightarrow{BC}$的夹角为60°，$\overrightarrow{BC}$=2$\overrightarrow{BD}$，且AD=2．∠ADC=120°，则$|{\overrightarrow{BA}+\overrightarrow{BC}}|$=（　　）

• A． 2$\sqrt{3}$
• B． 2$\sqrt{6}$
• C． 2$\sqrt{7}$
• D． 6

Answer 1

分析 根据已知条件容易得到D为边BC的中点，△ABD为等边三角形，从而可得到AB=2，BC=4，从而要求$|\overrightarrow{BA}+\overrightarrow{BC}|$先来求$（\overrightarrow{BA}+\overrightarrow{BC}）^{2}$，从而得出答案．

解答 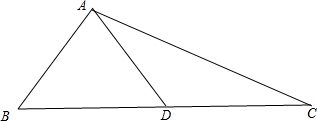解：如图，
由$\overrightarrow{BC}=2\overrightarrow{BD}$知，D是BC边的中点；
∠ADC=120°；
∴∠ADB=60°；
又∠ABD=60°；
∴△ABD是等边三角形，AD=2；
∴AB=2，BC=4；
∴$（\overrightarrow{BA}+\overrightarrow{BC}）^{2}={\overrightarrow{BA}}^{2}+2\overrightarrow{BA}•\overrightarrow{BC}$$+{\overrightarrow{BC}}^{2}=4+8+16=28$；
∴$|\overrightarrow{BA}+\overrightarrow{BC}|=2\sqrt{7}$．
故选：C．

点评 考查向量数乘的几何意义，等边三角形的概念，求向量长度的方法：先去求向量的平方，以及数量积的计算公式．