
分析 (Ⅰ)利用等比数列{an}满足an+1+an=9•2n-1,确定数列的公比与首项,即可求数列{an}的通项公式;
(Ⅱ)利用错误相减法求出Sn,再利用不等式Sn>kan-1,分离参数,求最值,即可求实数k的取值范围.
解答 解:(Ⅰ)设等比数列{an}的公比为q,
∵an+1+an=9•2n-1,
∴a2+a1=9,a3+a2=18,
∴q=$\frac{{a}_{3}+{a}_{2}}{{a}_{2}+{a}_{1}}$=$\frac{18}{9}$=2
又2a1+a1=9,∴a1=3.
∴an=3•2n-1. n∈N*.
(Ⅱ)bn=nan=3n•2n-1.
∴Sn=3×1×20+3×2×21+…+3(n-1)×2n-2+3n×2n-1,
∴$\frac{1}{3}$Sn=1×20+2×21+…+(n-1)×2n-2+n×2n-1,
∴$\frac{2}{3}$Sn=1×21+2×22+…+(n-1)×2n-1+n×2n,
∴-$\frac{1}{3}$Sn=1+21+22+…+2n-1-n×2n=$\frac{1-{2}^{n}}{1-2}$-n×2n=(1-n)2n-1,
∴Sn=3(n-1)2n+3,
∵Sn>kan-1对一切n∈N*恒成立,
∴k<$\frac{{S}_{n}+1}{{a}_{n}}$=$\frac{3(n-1){2}^{n}+4}{3•{2}^{n-1}}$=2(n-1)+$\frac{4}{3•{2}^{n-1}}$,
令f(n)=2(n-1)+$\frac{4}{3•{2}^{n-1}}$,
∴f′(n)=2+$\frac{8ln2}{3}$•($\frac{1}{2}$)n>0,
∴f(n)随n的增大而增大,
∴f(n)min=f(1)=$\frac{4}{3}$,
∴实数k的取值范围为(-∞,$\frac{4}{3}$).
点评 本题考查数列递推式,考查等比数列的通项与求和,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 分数大于等于120分 | 分数不足120分 | 合 计 | |
| 周做题时间不少于15小时 | 15 | 4 | 19 |
| 周做题时间不足15小时 | 10 | 16 | 26 |
| 合 计 | 25 | 20 | 45 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知命题p,q,若p∨(¬q)为真命题,则q一定是假命题 | |
| B. | 命题“?x∈R,2x>0”的否定是“$?{x_0}∈R,{2^{x_0}}<0$” | |
| C. | “$x=\frac{π}{4}$”是“tan x=l”的充分不必要条件 | |
| D. | “若x1>1,x2>1,则x1+x2>2”的否命题是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
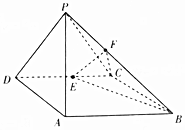 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
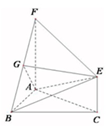 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF平行且等于2CE,G是线段BF上的一点,AB=AF=BC=2.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF平行且等于2CE,G是线段BF上的一点,AB=AF=BC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com