
分析 (1)对过其中两点作一直线中的两个点如何取进行分类讨论,一类两点全是共线中的4点,一类在共线中的4点任取一点,从4个共线之外的5个点,另一类共线中的4点不取,从4个共线之外的5个点选2个即可.
(2)任取两点都有两点都有2条射线,问题得以解决,
(3)分三类,从4个共线之外的5个点人选3个,从共线中的4点选1个,从共线中的4点选2个
解答 解:(1):共线中的4点任取两点构成同一直线,1条;
在共线中的4点任取1点,从4个共线之外的5个点选1个点,可构成4×5=20条;
在共线中的4点不取,从4个共线之外的5个点人选2个点,可构成C52=10条;
故一共1+20+10=31条.
(2)任取两点都有两点都有2条射线,共有A92=72条,
(3)从4个共线之外的5个点人选3个,故有C53=10个圆,
从共线中的4点选1个,从4个共线之外的5个点人选2个,故有C41C52=40个,
从共线中的4点选2个,从4个共线之外的5个点人选1个,故有C42C51=30个,
故一共10+40+30=80个,
点评 本题主要考查了空间中直线与直线之间的位置关系以及圆的个数问题,培养学生空间想象能力,属于中档题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{27}{2}$ | B. | 27 | C. | $27\sqrt{2}$ | D. | $27\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
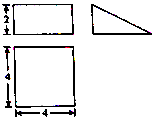
| A. | 32+8$\sqrt{5}$ | B. | 36π | C. | 18π | D. | $\frac{40\sqrt{10}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com