
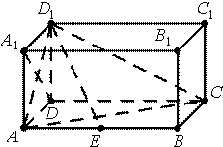
 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.| π |
| 4 |
| DA1 |
| D1E |
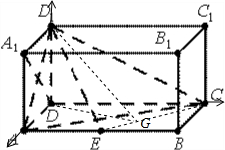 解:(1)以D为坐标原点,DA,DC,DD1所在的直线分别为x,y,z轴建立空间直角坐标系,
解:(1)以D为坐标原点,DA,DC,DD1所在的直线分别为x,y,z轴建立空间直角坐标系,| DA1 |
| D1E |
| DA1 |
| D1E |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,且AB=2
如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,且AB=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)查看答案和解析>>
科目:高中数学 来源: 题型:
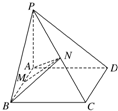 如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°.
如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com