
分析 根据|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{AB}$-$\overrightarrow{AC}$|得出$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,建立平面直角坐标系,利用平面向量的坐标运算表示出$\overrightarrow{AP}$•$\overrightarrow{AE}$,根据坐标运算即可求出$\overrightarrow{AP}$•$\overrightarrow{AE}$的取值范围.
解答 解:△ABC中,AB=AC=1,|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{AB}$-$\overrightarrow{AC}$|,∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,∴$\overrightarrow{AB}$⊥$\overrightarrow{AC}$;
以AC,AB为坐标轴建立平面直角坐标系,如图所示: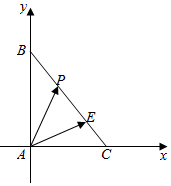
则A(0,0),C(1,0),B(0,1),
∵$\overrightarrow{BE}$=3$\overrightarrow{EC}$,∴E($\frac{3}{4}$,$\frac{1}{4}$);
直线BC方程为x+y=1,即x+y-1=0;
设P(x,y),则0≤x≤1,
则$\overrightarrow{AP}$=(x,y),$\overrightarrow{AE}$=($\frac{3}{4}$,$\frac{1}{4}$),
∴$\overrightarrow{AP}$•$\overrightarrow{AE}$=$\frac{3}{4}$x+$\frac{1}{4}$y=$\frac{3}{4}$x+$\frac{1}{4}$(1-x)=$\frac{1}{2}$x+$\frac{1}{4}$;
∵0≤x≤1,∴$\frac{1}{4}$≤$\frac{1}{2}$x+$\frac{1}{4}$≤$\frac{3}{4}$;
即$\overrightarrow{AP}$•$\overrightarrow{AE}$的取值范围是[$\frac{1}{4}$,$\frac{3}{4}$].
故答案为:[$\frac{1}{4}$,$\frac{3}{4}$].
点评 本题考查了平面向量的数量积运算,建立坐标系使用坐标计算是常用方法.


科目:高中数学 来源: 题型:选择题
 如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}}$)图象的一部分,为了得到这个函数的图象,只要将y=sinx的图象上所有的点( )
如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}}$)图象的一部分,为了得到这个函数的图象,只要将y=sinx的图象上所有的点( )| A. | 向左平移$\frac{π}{8}$个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 | |
| B. | 向右平移$\frac{π}{8}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变 | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变 | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.
如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
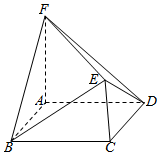 如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.
如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com