
分析 由条件可得α+β=kπ,k∈Z,若α+β=2nπ,n∈Z,则sinα=-sinβ,化简 sin(α+2β)为 sinβ+sinα=0.若α+β=(2n-1)π,n∈Z,则sinα=sinβ,化简 sin(α+2β)为-sinβ+sinα=0,从而证得结论.
解答 证明:∵tan(α+β)=0,∴sin(α+β)=0,cos(α+β)=±1,α+β=kπ,k∈Z,
若α+β=2nπ,n∈Z,则sin(α+β)=0,cos(α+β)=1,sinα=sin(2nπ-β)=-sinβ,
∴sin(α+2β)+sinα=sin(α+β)cosβ+cos(α+β)sinβ+sinα=sinβ+sinα=0.
若α+β=(2n-1)π,n∈Z 可得α=(2n-1)π-β,∴sinα=sin(2nπ-π-β)=sinβ,
sin(α+2β)+sinα=sin(α+β)cosβ+cos(α+β)sinβ+sinα=-sinβ+sinα=0,
综上可得,sin(α+2β)+sinα=0.
点评 本题主要考查两角和差的正弦公式,同角三角的基本关系,属于中档题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2或x>3} | B. | {x|x<-3或x>2} | C. | {x|-2<x<3} | D. | {x|-3<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{f(x)}$ | B. | y=lg[1-f(x)] | C. | y=${\frac{1}{2}}^{f(x)}$ | D. | y=|f(x)| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AC}$+$\overrightarrow{BA}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AC}$+$\overrightarrow{AD}$=$\overrightarrow{DC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
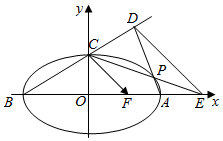 如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.
如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com