练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    化简：sin2α-
    sinαcosα
    sin2α
    +cos2α
    考点：同角三角函数基本关系的运用
    专题：三角函数的求值
    分析：原式1、3项结合，利用同角三角函数间的基本关系化简，第2项约分后利用同角三角函数间的基本关系化简，计算即可得到结果．
    解答： 解：原式=sin2α+cos2α-
    cosα
    sinα
    =1-cotα．
    点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设k=
    ∫
    π
    0
    （sinx-cosx）dx，若（1-kx）8=a0+a1x+a2x2+…+a8x8，则a1+a2+a3+…+a8=（　　）
    A、-1B、0C、lD、256

    查看答案和解析>>

    科目：高中数学 来源： 题型：

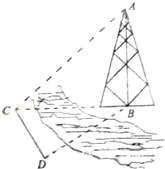    如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个侧点C与D．现测得∠BCD=60°，∠BDC=75°，CD=50
    		2
    ，并在点C测得塔顶A的仰角为60°，求塔高AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合A={x-y，x+y，xy}，B={x2+y2，x2-y2，0}，且A⊆B，B⊆A，求实数x，y的值和集合A、B．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=xekx（k≠0），求函数f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    F（x）=sin（x+
    7π
    4
    ）+cos（x-
    3π
    4
    ），（x∈R）
    （1）求F（x）的最小正周期、最小值、图象对称轴方程；
    （2）若cos（α-β）=
    4
    5
    ，cos（α+β）=-
    4
    5
    ，0＜α＜β≤
    π
    2
    ，求F2（β）-2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，把一些长度均为4米（PA+PB=4米）的铁管折弯后当作骨架制作“人字形”帐蓬，根据人们的生活体验知道：人在帐蓬里“舒适感”k与三角形的底边长和底边上的高度有关，设AB为x，AB边上的高PH为y，则k
    x+y
    		x2+y2
    ，若k越大，则“舒适感”越好．
    （Ⅰ）求“舒适感”k的取值范围；
    （Ⅱ）已知M是线段AB的中点，H在线段AB上，设MH=t，当人在帐蓬里的“舒适感”k达到最大值时，求y关于自变量t的函数解析式；并求出y的最大值（请说明详细理由）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A（3，0），B（0，3），C（cosα，sinα）．
    （1）若（2
    OA
    -
    OB
    ）⊥
    OC
    ，求cos2α；
    （2）若|
    OA
    +
    OC
    |=
    		13
    ，且α∈（0，π），求
    OB
    ，
    OC
    夹角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，sinA=
    3
    4
    ，∠C=30°，BC=3，则AB等于
     
    ．

    查看答案和解析>>

    同步练习册答案