考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质,平面向量及应用
分析:由三角函数中的恒等变换应用化简函数解析式可得f(x)=
sin(2x+
)-1,
①由2kπ+
≤2x+
≤2kπ+
,k∈Z可解得f(x)的单调递减区间,即可判断;
②由于解得f(
)=-1,故不是函数的对称中心;
③由2x+
=
-(2x+
),由诱导公式即可证明命题正确;
④根据函数的周期T=
=π,函数值等于0的x之差的最小值为
,所以x
1-x
2必是
的整数倍,即可判断.
解答:
解:f(x)=|
|=2sinxcosx-2sin
2x=
sin(2x+
)-1,
①由2kπ+
≤2x+
≤2kπ+
,k∈Z可解得f(x)的单调递减区间为:[kπ
+,kπ
+],k∈Z,故当k=0时,f(x)在区间[
,
]上是减函数,命题①正确;
②由于f(
)=
sin(2×
+
)-1=-1,故命题②错误;
③由于f(x)=
sin(2x+
)-1=
cos[
-(2x+
)]-1=
cos(2x-
)-1,故命题③正确;
④因为函数的周期T=
=π,函数值等于0的x之差的最小值为
,所以x
1-x
2必是
的整数倍.所以命题错误.
故答案为:①③.
点评:本题主要考查了平面向量及应用,三角函数的图象与性质,三角函数中的恒等变换应用,属于基本知识的考查.



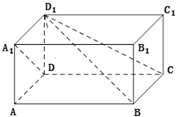 在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,侧棱DD1⊥平面ABCD,且AD=AA1=1,AB=2.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,侧棱DD1⊥平面ABCD,且AD=AA1=1,AB=2.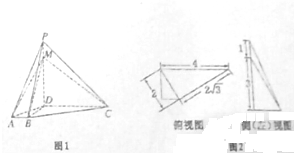 如图1,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,M为侧棱PD上一点,且该四棱锥的俯视图和侧(左)是图如图2所示.
如图1,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,M为侧棱PD上一点,且该四棱锥的俯视图和侧(左)是图如图2所示.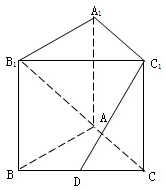 如图,在三棱柱ABC-A1B1C1中,侧棱与底面垂直,已知AB=AC=AA1=2,
如图,在三棱柱ABC-A1B1C1中,侧棱与底面垂直,已知AB=AC=AA1=2,