
分析 由平面向量坐标运算法则,求出$\overrightarrow{AB}$=(4,-1),$\overrightarrow{AF}$=$\overrightarrow{AB}+\overrightarrow{BF}$,$\overrightarrow{EF}$=$\overrightarrow{EA}+\overrightarrow{AF}$=($\frac{8}{3}$,-$\frac{2}{3}$),从而$\overrightarrow{EF}=\frac{2}{3}\overrightarrow{AB}$,由此能证明$\overrightarrow{EF}$∥$\overrightarrow{AB}$.
解答 证明:∵A,B,C三点的坐标为(-1,0),(3,-1),(1,2),
并且$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AC}$,$\overrightarrow{BF}$=$\frac{1}{3}$$\overrightarrow{BC}$,
∴$\overrightarrow{AE}$=$\frac{1}{3}(2,2)=(\frac{2}{3},\frac{2}{3})$,$\overrightarrow{BF}$=$\frac{1}{3}(-2,3)=(-\frac{2}{3},1)$,
$\overrightarrow{AB}$=(4,-1),$\overrightarrow{AF}$=$\overrightarrow{AB}+\overrightarrow{BF}$=(4,-1)+(-$\frac{2}{3}$,1)=($\frac{10}{3}$,0),
$\overrightarrow{EF}$=$\overrightarrow{EA}+\overrightarrow{AF}$=(-$\frac{2}{3},-\frac{2}{3}$)+($\frac{10}{3}$,0)=($\frac{8}{3}$,-$\frac{2}{3}$),
∴$\overrightarrow{EF}=\frac{2}{3}\overrightarrow{AB}$,
∴$\overrightarrow{EF}$∥$\overrightarrow{AB}$.
点评 本题考查向量平行的证明,是基础题,解题时要认真审题,注意平面向量坐标运算法则的合理运用.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰或直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
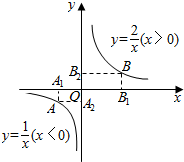 如图,动点A在函数y=$\frac{1}{x}$(x<0)的图象上,动点B在函数y=$\frac{2}{x}$(x>0)的图象上,过点A、B分别向x轴、y轴作垂线,垂足分别为A1、A2、B1、B2,若|A1B1|=4,则|A2B2|的最小值为$\frac{3+2\sqrt{2}}{4}$.
如图,动点A在函数y=$\frac{1}{x}$(x<0)的图象上,动点B在函数y=$\frac{2}{x}$(x>0)的图象上,过点A、B分别向x轴、y轴作垂线,垂足分别为A1、A2、B1、B2,若|A1B1|=4,则|A2B2|的最小值为$\frac{3+2\sqrt{2}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com