
【题目】设函数![]() (
(![]() ).
).
(1)试讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,记
,记![]() ,当
,当![]() 时,若函数
时,若函数![]() 与函数
与函数![]() 有两个不同交点
有两个不同交点![]() ,
,![]() ,设线段的中点为
,设线段的中点为![]() ,试问s是否为
,试问s是否为![]() 的根?说明理由.
的根?说明理由.
【答案】(1)见解析;(2)s不是![]() 的根,理由见解析
的根,理由见解析
【解析】
(1)求解函数的导函数,分类讨论可得:①若![]() 时,当
时,当![]() 时,函数
时,函数![]() 单调递减,当
单调递减,当![]() 时,函数
时,函数![]() 单调递增; ②若
单调递增; ②若![]() 时,函数
时,函数![]() 单调递增; ③若
单调递增; ③若![]() 时,当
时,当![]() 时,函数
时,函数![]() 单调递减,当
单调递减,当![]() 时,函数
时,函数![]() 单调递增.
单调递增.
(2)构造新函数![]() ,
,![]() 求解导函数可得
求解导函数可得![]() ,欲证
,欲证![]() ,故只需证明.
,故只需证明.![]() , 由于
, 由于![]() ,
,![]() 是方程
是方程![]() 的两个不相等的实根,不妨设为
的两个不相等的实根,不妨设为![]() ,代入方程化简可得
,代入方程化简可得![]() ,故只需证明
,故只需证明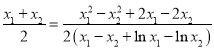 ,化简为
,化简为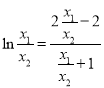 ,构造
,构造 ![]() ,
,![]() ,通过求导可知
,通过求导可知![]() 在
在![]() 单调递增.又
单调递增.又![]() ,因此
,因此![]() 即可证明
即可证明![]() 不成立.
不成立.
(1)由![]() ,可知
,可知![]() .
.
因为函数![]() 的定义域为
的定义域为![]() ,所以,
,所以,
①若![]() 时,当
时,当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
②若![]() 时,当
时,当![]() 在
在![]() 内恒成立,函数
内恒成立,函数![]() 单调递增;
单调递增;
③若![]() 时,当
时,当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
(2)证明:由题可知![]() (
(![]() ),
),
所以![]()
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
欲证![]() ,故只需证明.
,故只需证明.![]()
设![]() ,
,![]() 是方程
是方程![]() 的两个不相等的实根,不妨设为
的两个不相等的实根,不妨设为![]() ,
,
则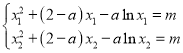
两式相减并整理得![]() ,
,
从而![]() ,
,
故只需证明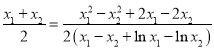 (*)
(*)
即![]() .所以(*)式可化为
.所以(*)式可化为![]() ,即
,即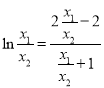
因为![]() ,所以
,所以![]() ,不妨令
,不妨令![]() ,即证
,即证![]() ,
,![]() 成立.
成立.
记![]() ,
,![]() ,所以
,所以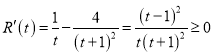 ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
因此![]() 在
在![]() 单调递增.又
单调递增.又![]() ,因此
,因此![]() ,
,![]() ,故
,故![]() ,
,![]() ,即
,即![]() 不成立.
不成立.
故s不是![]() 的根得证.
的根得证.


科目:高中数学 来源: 题型:
【题目】新型冠状病毒属于![]() 属的冠状病毒,人群普遍易感,病毒感染者一般有发热咳嗽等临床表现,现阶段也出现无症状感染者.基于目前的流行病学调查和研究结果,病毒潜伏期一般为1-14天,大多数为3-7天.为及时有效遏制病毒扩散和蔓延,减少新型冠状病毒感染对公众健康造成的危害,需要对与确诊新冠肺炎病人接触过的人员进行检查.某地区对与确诊患者有接触史的1000名人员进行检查,检查结果统计如下:
属的冠状病毒,人群普遍易感,病毒感染者一般有发热咳嗽等临床表现,现阶段也出现无症状感染者.基于目前的流行病学调查和研究结果,病毒潜伏期一般为1-14天,大多数为3-7天.为及时有效遏制病毒扩散和蔓延,减少新型冠状病毒感染对公众健康造成的危害,需要对与确诊新冠肺炎病人接触过的人员进行检查.某地区对与确诊患者有接触史的1000名人员进行检查,检查结果统计如下:
发热且咳嗽 | 发热不咳嗽 | 咳嗽不发热 | 不发热也不咳嗽 | |
确诊患病 | 200 | 150 | 80 | 30 |
确诊未患病 | 150 | 150 | 120 | 120 |
(1)能否在犯错率不超过0.001的情况下,认为新冠肺炎密切接触者有发热症状与最终确诊患病有关.
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.645 | 7.879 | 10.828 |
(2)在全国人民的共同努力下,尤其是全体医护人员的辛勤付出下,我国的疫情得到较好控制,现阶段防控重难点主要在境外输入病例和无症状感染者(即无相关临床表现但核酸检测或血清特异性免疫球蛋白M抗体检测阳者).根据防控要求,无症状感染者虽然还没有最终确诊患2019新冠肺炎,但与其密切接触者仍然应当采取居家隔离医学观察14天,已知某人曾与无症状感染者密切接触,而且在家已经居家隔离10天未有临床症状,若该人员居家隔离第![]() 天出现临床症状的概率为
天出现临床症状的概率为![]() ,
,![]() ,两天之间是否出现临床症状互不影响,而且一旦出现临床症状立刻送往医院核酸检查并采取必要治疗,若14天内未出现临床症状则可以解除居家隔离,求该人员在家隔离的天数(含有临床症状表现的当天)
,两天之间是否出现临床症状互不影响,而且一旦出现临床症状立刻送往医院核酸检查并采取必要治疗,若14天内未出现临床症状则可以解除居家隔离,求该人员在家隔离的天数(含有临床症状表现的当天)![]() 的分布列以及数学期望值.(保留小数点后两位)
的分布列以及数学期望值.(保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
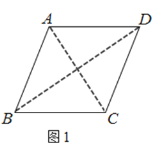
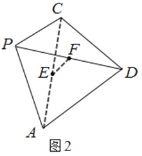
【题目】已知四边形![]() 是边长为5的菱形,对角线
是边长为5的菱形,对角线![]() (如图1),现以
(如图1),现以![]() 为折痕将菱形折起,使点
为折痕将菱形折起,使点![]() 达到点
达到点![]() 的位置,棱
的位置,棱![]() ,
,![]() 的中点分为
的中点分为![]() ,
,![]() ,且四面体
,且四面体![]() 的外接球球心落在四面体内部(如图2),则线段
的外接球球心落在四面体内部(如图2),则线段![]() 长度的取值范围为________.
长度的取值范围为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义行列式的运算如下: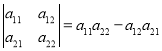 ,已函数
,已函数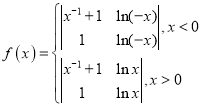 以下命题正确的是( )
以下命题正确的是( )
①对![]() ,都有
,都有![]() ;②若
;②若![]() ,对
,对![]() ,总存在非零常数了,使得
,总存在非零常数了,使得![]() ;③若存在直线
;③若存在直线![]() 与
与![]() 的图象无公共点,且使
的图象无公共点,且使![]() 的图案位于直线两侧,此直线即称为函数
的图案位于直线两侧,此直线即称为函数![]() 的分界线.则
的分界线.则![]() 的分界线的斜率的取值范围是
的分界线的斜率的取值范围是![]() ;④函数
;④函数![]() 的零点有无数个.
的零点有无数个.
A.①③④B.①②④
C.②③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“今年我已经8个月没有戏拍了”迪丽热巴在8月的一档综艺节目上说,霍建华在家里开玩笑时说到“我失业很久了”;明道也在参加《演员请就位》时透露,已经大半年没有演过戏.为了了解演员的生存现状,什么样的演员才有戏演,有人搜集了内地、港澳台共计9481名演员的演艺生涯资料,在统计的所有演员资料后得到以下结论:①有![]() 的人在2019年没有在影剧里露过脸;②2019年备案的电视剧数量较2016年时下滑超过三分之一;③女演员面临的竞争更加激烈;④演员的艰难程度随着年龄的增加而降低.请问:以下判断正确的是( )
的人在2019年没有在影剧里露过脸;②2019年备案的电视剧数量较2016年时下滑超过三分之一;③女演员面临的竞争更加激烈;④演员的艰难程度随着年龄的增加而降低.请问:以下判断正确的是( )
A.调查采用了分层抽样B.调查采用了简单随机抽样
C.调查采用了系统抽样D.非抽样案例
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() .若
.若![]() 为线段
为线段![]() 的中点.
的中点.
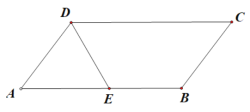
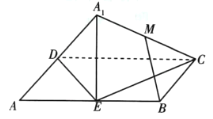
(1)证明![]() 平面
平面![]() ,并求
,并求![]() 的长;
的长;
(2)在翻折过程中,当三棱锥![]() 的体积取最大时,求平面
的体积取最大时,求平面![]() 与平面
与平面![]() 所成的二面角的余弦值.
所成的二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() (其中
(其中![]() ,点P的轨迹记为曲线
,点P的轨迹记为曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线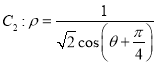 上.
上.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() ,
,![]() 时,求曲线
时,求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标
的公共点的极坐标
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com