
| A�� | ��-$\frac{��}{6}$��$\frac{1}{2}$�� | B�� | ��$\frac{��}{6}$��$\frac{1}{2}$�� | C�� | ��$\frac{��}{3}$��$\frac{3}{2}$�� | D�� | ��-$\frac{��}{3}$��$\frac{3}{2}$�� |
���� ���ú���y=Asin����x+�գ���ͼ��任���ɣ����Һ����ĵ������Լ��������ֵ����һ�������ѡ���Ƿ���ȷ���Ӷ��ó����ۣ�
��� 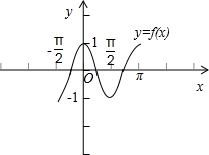 �⣺�ѽ�����f��x��=cos2x��x��R����ͼ��������$\overrightarrow{a}$=��-$\frac{��}{6}$��$\frac{1}{2}$��
�⣺�ѽ�����f��x��=cos2x��x��R����ͼ��������$\overrightarrow{a}$=��-$\frac{��}{6}$��$\frac{1}{2}$��
ƽ�ƺɵ�y=cos��2x+$\frac{��}{3}$��+$\frac{1}{2}$��ͼ��
��x��[$\frac{��}{3}$��$\frac{2��}{3}$]ʱ��2x+$\frac{��}{3}$��[�У�$\frac{5��}{3}$]��
���ú���y=cos��2x+$\frac{2��}{3}$��Ϊ��������
�ҵ�2x+$\frac{��}{3}$=$\frac{5��}{3}$ʱ������f��x��ȡ�����ֵΪ$\frac{1}{2}$+$\frac{1}{2}$=1��
������������A�ʺ����⣮
�ѽ�����f��x��=cos2x��x��R����ͼ��������$\overrightarrow{a}$=��$\frac{��}{6}$��$\frac{1}{2}$��
ƽ�ƺɵ�y=cos��2x-$\frac{��}{3}$��+$\frac{1}{2}$��ͼ��
��x��[$\frac{��}{3}$��$\frac{2��}{3}$]ʱ��2x-$\frac{��}{3}$��[$\frac{��}{3}$����]��
���ú���y=cos��2x+$\frac{2��}{3}$��+$\frac{1}{2}$Ϊ�����������ֵΪ$\frac{1}{2}$+$\frac{1}{2}$=1�����������������ų�B��
�ѽ�����f��x��=cos2x��x��R����ͼ��������$\overrightarrow{a}$=��$\frac{��}{3}$��$\frac{3}{2}$��ƽ�ƺɵ�y=cos��2x-$\frac{2��}{3}$��+$\frac{3}{2}$��ͼ��
��x��[$\frac{��}{3}$��$\frac{2��}{3}$]ʱ��2x-$\frac{2��}{3}$��[0��$\frac{2��}{3}$]��
���ú���y=cos��2x-$\frac{2��}{3}$��+$\frac{3}{2}$Ϊ�����������ֵΪ1+$\frac{3}{2}$=$\frac{5}{2}$�����������������ų�C��
�ѽ�����f��x��=cos2x��x��R����ͼ��������$\overrightarrow{a}$=��-$\frac{��}{3}$��$\frac{3}{2}$��ƽ�ƺɵ�y=cos��2x+$\frac{2��}{3}$��+$\frac{3}{2}$��ͼ��
��x��[$\frac{��}{3}$��$\frac{2��}{3}$]ʱ��2x-$\frac{��}{3}$��[$\frac{��}{3}$����]��
���ú���y=cos��2x+$\frac{2��}{3}$��+$\frac{3}{2}$Ϊ�����������ֵΪ$\frac{1}{2}$+$\frac{3}{2}$=2�����������������ų�D��
��ѡ��A��
���� ������Ҫ�������Һ�����ͼ������������y=Acos����x+�գ���ͼ��任���ɣ����ڻ����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-1����2��+�ޣ� | B�� | ��2��+�ޣ� | C�� | ��-�ޣ�-1�� | D�� | ��-1��2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com