
分析 (Ⅰ)设圆C的圆心坐标为(a,a),利用CA=CB,建立方程,求出a,即可求圆C的方程;
(Ⅱ)分类讨论,利用圆心到直线的距离公式,求出斜率,即可得出直线方程.
解答 解:(Ⅰ)设圆C的圆心坐标为(a,a),
依题意,有$\sqrt{{{(a-1)}^2}+{{(a-3)}^2}}=\sqrt{{{(a+1)}^2}+{{(a-1)}^2}}$,
即a2-6a+9=a2+2a+1,解得a=1,(2分)
所以r2=(1-1)2+(3-1)2=4,(4分)
所以圆C的方程为(x-1)2+(y-1)2=4.(5分)
(Ⅱ)依题意,圆C的圆心到直线l的距离为1,
所以直线x=2符合题意.(6分)
设直线l方程为y+2=k(x-2),即kx-y-2k-2=0,
则$\frac{|k+3|}{{\sqrt{{k^2}+1}}}=1$,解得$k=-\frac{4}{3}$,
所以直线l的方程为$y+2=-\frac{4}{3}(x-2)$,即4x+3y-2=0.(9分)
综上,直线l的方程为x-2=0或4x+3y-2=0.(10分)
点评 本题考查圆的标准方程,考查直线与圆的位置关系,考查学生的计算能力,正确运用点到直线的距离公式是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
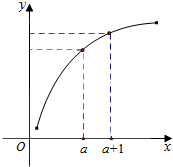
| A. | 0<f′(a)<f′(a+1)<f(a+1)-f(a) | B. | 0<f′(a+1)<f(a+1)-f(a)<f′(a) | ||
| C. | 0<f′(a+1)<f′(a)<f(a+1)-f(a) | D. | 0<f(a+1)-f(a)<f′(a)<f′(a+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | (0,1) | C. | [1,3) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
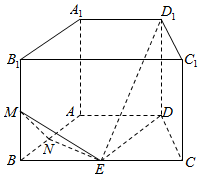 如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.
如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com