
 满足条件:存在正整数
满足条件:存在正整数 ,使得
,使得 对一切
对一切 都成立,则称数列
都成立,则称数列 为
为 级等比数列.
级等比数列. 为2级等比数列,且前四项分别为
为2级等比数列,且前四项分别为 ,求
,求 的值;
的值; 为常数),且
为常数),且 是
是 级等比数列,求
级等比数列,求 所有可能值的集合,并求
所有可能值的集合,并求 取最小正值时数列
取最小正值时数列 的前
的前 项和
项和 ;
; 为等比数列的充要条件是
为等比数列的充要条件是 既为
既为 级等比数列,
级等比数列, 也为
也为 级等比数列.
级等比数列.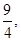 (2)
(2)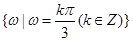 ,0,(3)详见解析.
,0,(3)详见解析.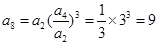 ,
,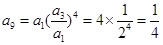 ,
,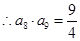 ,(2)本题化简是关键.因为
,(2)本题化简是关键.因为 是
是 级等比数列,所以
级等比数列,所以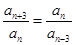
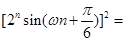
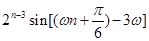
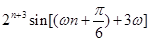
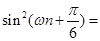
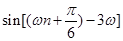

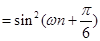
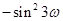
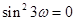 ,
,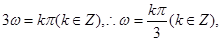
 最小正值等于
最小正值等于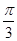 ,此时
,此时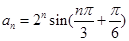
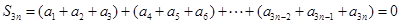 ,(3)充分性就是验证,易证,关键在于证必要性,可从两者中在交集(共同元素)出发.
,(3)充分性就是验证,易证,关键在于证必要性,可从两者中在交集(共同元素)出发. 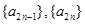 ,
, 成等比数列, 因此
成等比数列, 因此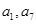 既是
既是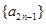 中的项,也是
中的项,也是 中的项,
中的项,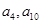 既是
既是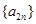 中的项,也是中
中的项,也是中 的项,可得它们公比的关系,进而推出三者结构统一,得出等比数列的结论.
的项,可得它们公比的关系,进而推出三者结构统一,得出等比数列的结论.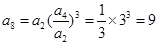 (2分)
(2分)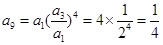
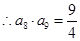 (4分)
(4分) 是
是 级等比数列,
级等比数列,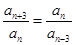
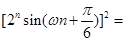
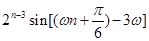
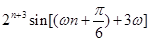 (1分)
(1分)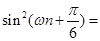
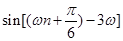

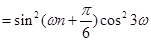

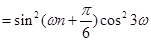

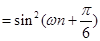
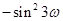
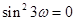 ,
,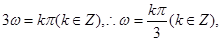
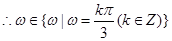 (3分)
(3分) 最小正值等于
最小正值等于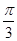 ,此时
,此时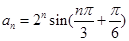
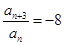 ,
,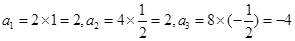 ,
,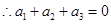
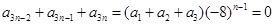 (5分)
(5分)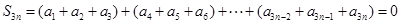 (6分)
(6分) 为等比数列,则
为等比数列,则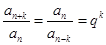
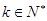 成立,显然对
成立,显然对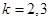 成立。
成立。 既为
既为 级等比数列,
级等比数列, 也为
也为 级等比数列。 (2分)
级等比数列。 (2分) 为
为 级等比数列,
级等比数列,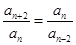 ,则
,则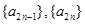 均成等比数列,设等比数列
均成等比数列,设等比数列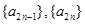 的公比分别为
的公比分别为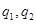 ,
, 为
为 级等比数列,
级等比数列,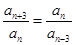 ,则
,则 成等比数列,设公比为
成等比数列,设公比为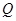 (3分)
(3分)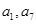 既是中
既是中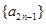 的项,也是
的项,也是 中的项,
中的项,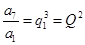
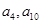 既是中
既是中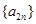 的项,也是中
的项,也是中 的项,
的项,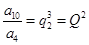
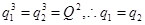 (5分)
(5分)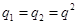 ,则
,则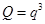
 (
(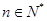 ),
),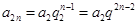 (
(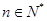 ),
),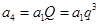 ,
,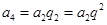 ,
, , (7分)
, (7分)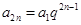 (
(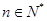 )
)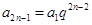 ,
,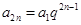 (
(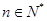 )
)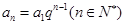 ,显然
,显然 为等比数列。 (8分)
为等比数列。 (8分)

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.-1 | B.0 | C.1 | D.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com