Question

3．三棱锥V-ABC的三条棱VA，VB，VC两两垂直，三个侧面与底面所成的二面角大小分别为α，β，γ．求证：$cosαcosβcosγ（{\frac{1}{{{{cos}^2}α}}+\frac{1}{{{{cos}^2}β}}+\frac{1}{{{{cos}^2}γ}}}）≥\sqrt{3}$．

Answer 1

分析 设三棱锥V-ABC的三条棱VA，VB，VC的长度分别为a、b、c，如图，过C作CD⊥AB于D，连结VD，三棱锥V-ABC的三条棱VA，VB，VC两两垂直，得∠VDC就是侧面VAB与地面ABC所成角α．cos²α=$\frac{1}{1+ta{n}^{2}α}=\frac{1}{1+（\frac{c}{VD}）^{2}}$=$\frac{{a}^{2}{b}^{2}}{{a}^{2}{b}^{2}+{a}^{2}{c}^{2}+{b}^{2}{c}^{2}}$；同理cos²β=$\frac{{a}^{2}{c}^{2}}{{a}^{2}{b}^{2}+{a}^{2}{c}^{2}+{b}^{2}{c}^{2}}$，cos²γ=$\frac{{b}^{2}{c}^{2}}{{a}^{2}{b}^{2}+{a}^{2}{c}^{2}+{b}^{2}{c}^{2}}$．cos²α+cos²β+cos²γ=1，再证$\frac{{a}^{2}+{b}^{2}+{c}^{2}}{\sqrt{{a}^{2}{b}^{2}+{a}^{2}{c}^{2}+{b}^{2}{c}^{2}}}≥\sqrt{3}$．

解答 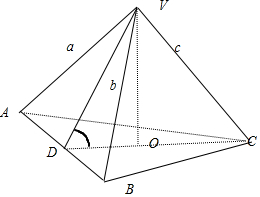解：设三棱锥V-ABC的三条棱VA，VB，VC的长度分别为a、b、c
如图，过C作CD⊥AB于D，连结VD，∵三棱锥V-ABC的三条棱VA，VB，VC两两垂直，∴VC⊥AB
∴AB⊥面VDC，∴∠VDC就是侧面VAB与地面ABC所成角α．
cos²α=$\frac{1}{1+ta{n}^{2}α}=\frac{1}{1+（\frac{c}{VD}）^{2}}$=$\frac{{a}^{2}{b}^{2}}{{a}^{2}{b}^{2}+{a}^{2}{c}^{2}+{b}^{2}{c}^{2}}$；
同理cos²β=$\frac{{a}^{2}{c}^{2}}{{a}^{2}{b}^{2}+{a}^{2}{c}^{2}+{b}^{2}{c}^{2}}$，cos²γ=$\frac{{b}^{2}{c}^{2}}{{a}^{2}{b}^{2}+{a}^{2}{c}^{2}+{b}^{2}{c}^{2}}$．
∴cos²α+cos²β+cos²γ=1，
所以要证：$cosαcosβcosγ（{\frac{1}{{{{cos}^2}α}}+\frac{1}{{{{cos}^2}β}}+\frac{1}{{{{cos}^2}γ}}}）≥\sqrt{3}$，只证$\frac{{a}^{2}+{b}^{2}+{c}^{2}}{\sqrt{{a}^{2}{b}^{2}+{a}^{2}{c}^{2}+{b}^{2}{c}^{2}}}≥\sqrt{3}$．只证${a}^{4}+{b}^{4}+{c}^{4}≥{a}^{2}{b}^{2}+\$a²c²+b²c²，
又因为：a⁴+b⁴≥2a²b²，a⁴+c⁴≥2a^2c2，c⁴+b⁴≥2c²b²，显然${a}^{4}+{b}^{4}+{c}^{4}≥{a}^{2}{b}^{2}+\$a²c²+b²c²，故原命题成立．

点评 本题考查了空间角，及证明不等式，转化思想是关键，属于难题．