
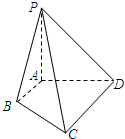
 如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.
如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.分析 (1)说明∠DPA是直线PD与平面PAB所成的角,然后计算求解即可.
(2)通过VB-PCD=VP-BCD,以及VP-BCD=$\frac{1}{3}×$S△PCD×d,求出d,即可得到点B到平面PCD的距离.
解答 解:(1)∵PA⊥平面ABCD,∴PA⊥AD,
又∵∠BAD=90°∴AD⊥平面PAB∴∠DPA是直线PD与平面PAB所成的角 …3分,
∵$∠DPA=\frac{π}{4}$,所以直线PD与平面PAB所成的角为$\frac{π}{4}$ …6分
(2)∵VB-PCD=VP-BCD…8分
而VP-BCD=$\frac{1}{3}×\frac{1}{2}×2×1×1$=$\frac{1}{3}$. …10分
PD=$\sqrt{2}$,S△PCD=$\sqrt{2}$,…12分
VP-BCD=$\frac{1}{3}×$S△PCD×d,所以d=$\frac{\sqrt{2}}{2}$,即点B到平面PCD的距离为$\frac{\sqrt{2}}{2}$ …14分.
点评 本题考查直线与平面市场价的求法,几何体的体积的应用,点到平面的距离的求法,考查空间想象能力以及计算能力.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:解答题
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | |||
| “不认可”手机 | |||
| 合计 |
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两条射线 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$,1 | B. | $\sqrt{2}$,5 | C. | ±$\sqrt{2}$,5 | D. | ±$\sqrt{2}$,1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com