
分析 (1)由题意可得:a2-b2=1,$\frac{(\frac{2}{3})^{2}}{{a}^{2}}$+$\frac{(\frac{2\sqrt{6}}{3})^{2}}{{b}^{2}}$=1,联立解出即可得出.
(2)ABCD为正方形,可得AC⊥BD,设直线AC的方程为:y=-x+m.代入椭圆方程可得:7x2-8mx+4m2-12=0,△>0,解得$-\sqrt{7}$<m$<\sqrt{7}$,设A(x1,y1),C(x2,y2),利用根与系数的关系、中点坐标公式可得:线段AC的中点M$(\frac{4m}{7},\frac{3m}{7})$.由点M在直线BD上,代入解得m=-1∈$(-\sqrt{7},\sqrt{7})$.可得直线AC的方程为:x+y+1=0.可得|AC|=$\sqrt{1+(-1)^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$.可得该正方形ABCD的面积S=$\frac{1}{2}|AC{|}^{2}$.
解答 解:(1)由题意可得:a2-b2=1,$\frac{(\frac{2}{3})^{2}}{{a}^{2}}$+$\frac{(\frac{2\sqrt{6}}{3})^{2}}{{b}^{2}}$=1,联立解得a2=4,b2=3.
∴椭圆P的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
(2)∵ABCD为正方形,∴AC⊥BD,设直线AC的方程为:y=-x+m.
代入椭圆方程可得:7x2-8mx+4m2-12=0,
△=64m2-28(4m2-12)>0,解得$-\sqrt{7}$<m$<\sqrt{7}$,
设A(x1,y1),C(x2,y2),
则x1+x2=$\frac{8m}{7}$,x1•x2=$\frac{4{m}^{2}-12}{7}$,y1+y2=2m-(x1+x2)=2m-$\frac{8m}{7}$=$\frac{6m}{7}$.
∴线段AC的中点M$(\frac{4m}{7},\frac{3m}{7})$.
由点M在直线BD上,∴7×$\frac{4m}{7}$-7×$\frac{3m}{7}$+1=0,解得m=-1∈$(-\sqrt{7},\sqrt{7})$.
∴直线AC的方程为:x+y+1=0.
|AC|=$\sqrt{1+(-1)^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$×$\sqrt{(-\frac{8}{7})^{2}-4×(-\frac{8}{7})}$=$\frac{24}{7}$.
∴该正方形ABCD的面积S=$\frac{1}{2}|AC{|}^{2}$=$\frac{1}{2}×(\frac{24}{7})^{2}$=$\frac{288}{49}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、一元二次方程的根与系数的关系、正方形的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
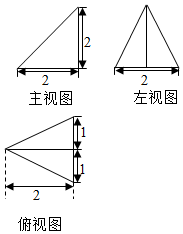 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{9}$ | C. | $\sqrt{6}-2$ | D. | $3\sqrt{6}-6$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $-\frac{7}{8}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∠MCN<θ | B. | ∠MCN=θ | ||
| C. | ∠MCN>θ | D. | 以上三种情况都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{3-2\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
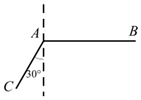 如图,当甲船位于A处时获悉,在其正东方向相距10海里的B处有个艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距6海里的C处的乙船,乙船立即朝北偏东(θ+30°)的方向沿直线前往B处营救,则sinθ的值为$\frac{5\sqrt{3}}{14}$.
如图,当甲船位于A处时获悉,在其正东方向相距10海里的B处有个艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距6海里的C处的乙船,乙船立即朝北偏东(θ+30°)的方向沿直线前往B处营救,则sinθ的值为$\frac{5\sqrt{3}}{14}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com