考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:不等式整理后,设f(x)=x2015-2014x2014,由φ的范围求出x的范围,确定出导函数大于0,进而得到cosφ大于sinφ,即可确定出φ的范围.
解答:
解:不等式cos
2015φ-sin
2015φ>2014(cos
2014φ-sin
2014φ),
整理得:cos
2015φ-2014cos
2014φ>sin
2015φ-2014sin
2014φ,
设f(x)=x
2015-2014x
2014,
∵φ∈[0,2π),
∴x∈[-1,1],
∵当x∈[-1,0)时,f′(x)=2015x
2014-2014
2x
2013=(2015x-2014
2)x
2013>0,此时函数为增函数,
∵f(cosφ)>f(sinφ),
∴cosφ>sinφ,
∴φ的取值范围是(
,2π);
当x∈[0,1)时,f′(x)=2015x
2014-2014
2x
2013=(2015x-2014
2)x
2013<0,此时函数为减函数,
∵f(cosφ)>f(sinφ),
∴cosφ<sinφ,
∴φ的取值范围是[
,
),
综上,φ的取值范围是[
,
)∪(
,2π).
故答案为:[
,
)∪(
,2π)
点评:此题考查了同角三角函数基本关系的运用,以及导函数的性质,熟练掌握导函数的性质是解本题的关键.



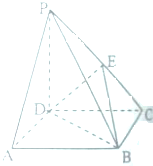 如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.