
 如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体外接球的表面积为( )| A. | $\frac{45}{4}$πcm2 | B. | 45πcm2 | C. | 54πcm2 | D. | 216πcm2 |
分析 由三视图知该几何体是三棱锥,由三视图得到直观图,求出外接球的半径,进一步求球的表面积.
解答 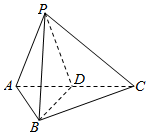 解:根据三视图和题意知几何体是三棱锥P-ABC,
解:根据三视图和题意知几何体是三棱锥P-ABC,
直观图如图所示:
D是AC的中点,PB⊥平面ABC,且PB=BD=3,所以AB=BC=3$\sqrt{2}$;
∴PB⊥AB,PB⊥BC,PB⊥BD,所以三棱锥外接球的直径为$\sqrt{P{B}^{2}+A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+(3\sqrt{2})^{2}+(3\sqrt{2})^{2}}$=3$\sqrt{5}$,
所以外接球的半径为$\frac{3\sqrt{5}}{2}$,表面积为4$π(\frac{3\sqrt{5}}{2})^{2}$=45π;
故选B.
点评 本题考查了由三视图求几何体的表面积,由三视图正确复原几何体是解题的关键,考查了空间想象能力.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:填空题
 如图,用四中不同的颜色给图中的A、B、C、D、E涂色,要求每个点涂一种颜色,且图中每条线段的两端点涂不同颜色,则不同的涂色方法有144种.
如图,用四中不同的颜色给图中的A、B、C、D、E涂色,要求每个点涂一种颜色,且图中每条线段的两端点涂不同颜色,则不同的涂色方法有144种.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 3i | C. | -3 | D. | -3i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | 1 | 2 | 3 | 4 |
| P | $\frac{2}{7}$ | $\frac{1}{7}$ | $\frac{5}{14}$ | p |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{14}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{10}{3}$,$\frac{7}{6}$) | B. | ($\frac{7}{6}$,$\frac{10}{3}$) | C. | (-$\frac{7}{6}$,$\frac{10}{3}$) | D. | (-$\frac{10}{3}$,-$\frac{7}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com