
已知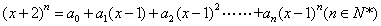 .
.
⑴求 及
及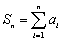 ;
;
⑵试比较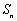 与
与 的大小,并说明理由.
的大小,并说明理由.
科目:高中数学 来源: 题型:
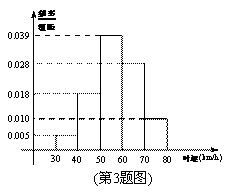
某时段内共有100辆汽车经过某一雷达测速区域,将测得的汽车时速绘制成如图所示
的频率分布直方图.根据图形推断,该时段时速超过50km/h的汽车辆数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆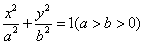 的左顶点为
的左顶点为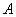 (-2,0),且过点
(-2,0),且过点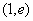 ,(e为椭圆的离心率);过
,(e为椭圆的离心率);过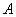 作两条互相垂直的弦
作两条互相垂直的弦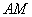 ,
,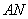 交椭圆于
交椭圆于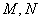 两点。
两点。
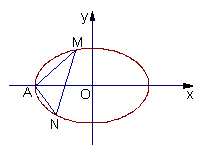 (1)求点椭圆的方程;
(1)求点椭圆的方程;
(2)求证:直线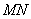 恒过
恒过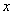 轴上的一个定点。
轴上的一个定点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com