练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知实数a≠0，函数f(x)＝ax(x－2)2 (x∈R)有极大值32.

    (1)求实数a的值；

    (2)求函数f(x)的单调区间．


    解　(1)∵f(x)＝ax3－4ax2＋4ax，

    ∴f′(x)＝3ax2－8ax＋4a＝a(3x－2)(x－2)．

    令f′(x)＝0，得x＝或x＝2.

    ∵f(x)＝ax(x－2)2 (x∈R)有极大值32，

    ∴当x＝时，f(x)取得极大值32，

    即a2＝32，∴a＝27.

    (2)由(1)知，f(x)＝27x(x－2)2，

    ∴f′(x)＝27(3x－2)(x－2)．

    令f′(x)>0，则x>2或x<；

    令f′(x)<0，则<x<2.

    所以函数f(x)的单调增区间是，(2，＋∞)；

    单调减区间是


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在△ABC中，∠C＝120°，tan A＋tan B＝，则tan Atan B的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知cos(π－α)＝，α∈，则tan α＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    扇形AOB的周长为8 cm.

    (1)若这个扇形的面积为3 cm2，求圆心角的大小；

    (2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x3＋ax2＋(a＋6)x＋1有极大值和极小值，则a的取值范围是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x3－x2－x，则f(－a2)与f(－1)的大小关系为      .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)是定义在[－1，0)∪(0，1]上的奇函数，当x∈[－1，0)时，f(x)＝2ax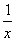＋(a为实数).

    (1)当x∈(0，1]时，求f(x)的解析式；

    (2)当a>－1时，试判断f(x)在(0，1]上的单调性，并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在某种新型材料的研制中，实验人员获得了下列一组实验数据：

    x

    1.99

    3

    4

    5.1

    6.12

    y

    1.5

    4.04

    7.5

    12

    18.01

    现准备用下列四个函数中的一个近似地表示这些数据的规律，其中最接近的一个是_____．

    ①y＝2x－2  ②y＝(x2－1)    ③y＝log3x  ④y＝2x－2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列命题中的假命题是________．

    ①∃x∈R，lg x＝0  ②∃x∈R，tan x＝1 ③∀x∈R，x3>0  ④∀x∈R,2x>0

    查看答案和解析>>

    同步练习册答案