Question

动圆C与定圆C₁：（x+3）²+y²=32内切，与定圆C₂：（x-3）²+y²=8外切，A点坐标为（0，

9

2

）．
（1）求动圆C的圆心C的轨迹方程和离心率；
（2）若轨迹C上的两点P，Q满足

AP

=5

AQ

，求|PQ|的值．

Answer 1

考点：轨迹方程,向量的模,椭圆的简单性质

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）根据两圆的位置关系，算出点C到C₁、C₂的距离之和等于6

2

，再由椭圆的定义可得C点的轨迹是以C₁，C₂为焦点的椭圆，结合题中数据即可得到所求轨迹方程；
（2）设P（x₁，y₁），Q（x₂，y₂），根据

AP

=5

AQ

，解出x₁=5x₂且y₁=5y₂-18，根据PQ都在椭圆C上，联解得出y₂=3，代入前面式子可得y₁=-3，且x₁=x₂=0，由此得出P、Q的坐标，从而得到|PQ|的值．

解答： 解：（1）如图，设动圆C的半径为R，
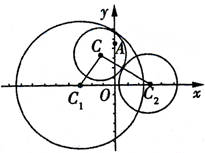
则|CC₁|=4

2

-R，…①，|CC₂|=2

2

+R，…②
①+②得，|CC₁|+|CC₂|=6

2

＞6=|C₁C₂|，
由椭圆的定义，C点的轨迹是以C₁，C₂为焦点，长轴长为6

2

的椭圆，
可得轨迹方程为

x2

18

+

y2

9

=1，离心率为

2

2

．
（2）设P（x₁，y₁），Q（x₂，y₂），则
∵

AP

=5

AQ

，
∴（x₁，y₁-

9

2

）=5（x₂，y₂-

9

2

），
可得x₁=5x₂，y₁=5y₂-18，…③
由P，Q是椭圆C上的两点，解出y₂=3
将y₂=3代入③，得y₁=-3，再将y₂=3代入④，得x₂=0，所以x₁=0，
∴P（0，-3），Q（0，3），可得|PQ|=6．

点评：本题给出动圆与两个定圆都相切，求圆心的轨迹方程并求满足向量等式的P、Q的坐标．着重考查了圆与圆的位置关系、向量的坐标运算和直线与圆锥曲线的位置关系等知识，属于中档题．