
分析 (1)设事件“选手在第三扇门使用求助且最终获得12000元家庭梦想基金”为事件A.利用独立重复试验求得概率.
(2)写出X的所有可能取值并求得其概率和分布列.
解答 解:设事件“该选手回答正确第i扇门的歌曲名称”为事件Ai,“使用求助回答正确歌曲名称”为事件B,
事件“每一扇门回答正确后选择继续挑战下一扇门”为事件C;则
$P({A}_{1})=\frac{5}{6},P({A}_{2})=\frac{4}{5},P({A}_{3})=\frac{3}{4}$,$P({A}_{4})=\frac{2}{3},P({A}_{5})=\frac{1}{2}$,$P(B)=\frac{1}{5},P(C)=\frac{1}{2}$…(2分)
(1)设事件“选手在第三扇门使用求助且最终获得12000元家庭梦想基金”为事件A,则:
A=A1CA2C $\overline{{A}_{3}}BC{A}_{4}\overline{C}=\frac{5}{6}×\frac{4}{5}×\frac{1}{4}×\frac{1}{5}×\frac{2}{3}$×$(\frac{1}{2})^{4}=\frac{1}{720}$
∴选手在第三扇门使用求助且最终获得12000元家庭梦想基金的概率为$\frac{1}{720}$;…(6分)
(2)X的所有可能取值为:0,3000,6000,8000,12000,24000;
P(X=3000)=P(A1$\overline{C}$)=$\frac{5}{6}×\frac{1}{2}=\frac{5}{12}$;
P(X=6000)=P(A1 CA2 $\overline{C}$)=$\frac{5}{6}$×$\frac{4}{5}$×($\frac{1}{2}$)2=$\frac{1}{6}$;
P(X=8000)=P(A1 CA2 CA3 $\overline{C}$)=$\frac{5}{6}×\frac{4}{5}×\frac{3}{4}×(\frac{1}{2})^{3}=\frac{1}{16}$;
P(X=12000)=P(A1 CA2 CA3 CA4 $\overline{C}$)=$\frac{5}{6}×\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×(\frac{1}{2})^{4}=\frac{1}{48}$;
P(X=24000)=P(A1 CA2 CA3 CA4 CA5)=$\frac{5}{6}×\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×(\frac{1}{2})^{5}=\frac{1}{96}$;
P(X=0)=P($\overline{{A}_{1}}$)+P(A1C $\overline{{A}_{2}}$)+P(A1CA2C $\overline{{A}_{3}}$)+P(A1CA2CA3C $\overline{{A}_{4}}$)+P(A1CA2CA3CA4C $\overline{{A}_{5}}$)=$\frac{1}{6}+\frac{1}{12}+\frac{1}{24}+\frac{1}{48}+\frac{1}{96}=\frac{31}{96}$;
(或P(X=0)=1-(P(X=3000)+P(X=6000)+P(X=8000)+P(X=12000)+P(X=24000)
=1-$(\frac{5}{12}+\frac{1}{6}+\frac{1}{16}+\frac{1}{48}+\frac{1}{96})=1-\frac{65}{96}=\frac{31}{96}$).
∴X的分布列为:
| X | 0 | 3000 | 6000 | 8000 | 12000 | 24000 |
| P | $\frac{31}{96}$ | $\frac{5}{12}$ | $\frac{1}{6}$ | $\frac{1}{16}$ | $\frac{1}{48}$ | $\frac{1}{96}$ |
点评 本题主要考查了独立重复试验和随机变量的期望,属中档题型,高考常考题型


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )| A. | 28 πcm3 | B. | 14πcm3 | C. | 7πcm3 | D. | 56πcm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
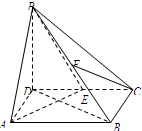 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}π}{2015}$ | B. | $\frac{2\sqrt{2}π}{2015}$ | C. | $\frac{2π}{2015}$ | D. | $\frac{4π}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
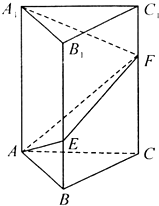 如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.
如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$或$-\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com