
分析 (1)由x的范围可得2x+$\frac{π}{6}$的范围,由最值可得可得ab的方程组,解方程组可得a,b的值;
(2)由-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,解得f(x)的单调递增区间,由$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,即可解得单调递减区间.
(3)根据函数y=Asin(ωx+φ)的图象变换规律即可得解.
解答 (本小题14分)
解:(1)∵x∈[0,$\frac{π}{2}$],
∴$\frac{π}{6}$≤2x+$\frac{π}{6}$≤$\frac{7}{6}$π,
∴-$\frac{1}{2}$≤sin(2x+$\frac{π}{6}$)≤1,
又∵a>0,-5≤f(x)≤1,
∴$\left\{\begin{array}{l}{-2a+2a+b=-5}\\{a+2a+b=1}\end{array}\right.$,
∴解得:$\left\{\begin{array}{l}{a=2}\\{b=-5}\end{array}\right.$,
(2)f(x)=-4sin(2x+$\frac{π}{6}$)-1,
由-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,得:-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z,
由$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,得:$\frac{π}{6}$+kπ≤x≤$\frac{2}{3}$π+kπ,k∈Z,
∴f(x)的单调递增区间为:[$\frac{π}{6}$+kπ,$\frac{2}{3}$π+kπ](k∈Z),单调递减区间为:[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ](k∈Z).
(3)将函数f(x)=sinx的图象向右移动$\frac{π}{6}$个单位,
再纵坐标不变横坐标缩短为原来的一半,
再横坐标不变纵坐标扩大为原来的4倍,
而后将图象关于x轴对称,然后将其再向下移动一个单位即可得到所求函数图象.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换,三角函数的最值,正弦函数的单调性,考查了数形结合思想,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 若x、y是实数,则x2≠y2?x≠y或x≠-y | |
| B. | 命题:“a,b都偶数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a,b都不是偶数” | |
| C. | 若“p或q”为假命题,则“非p且非q”是真命题 | |
| D. | 已知a,b,c是实数,关于x的不等式ax2+bx+c≤0的解集是空集,必有a>0且△≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 1或$\frac{1}{2}$ | D. | 1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e | B. | -e | C. | 2e | D. | -2e |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{4}$-$\frac{x^2}{5}$=1(y≤-2) | B. | $\frac{y^2}{4}$-$\frac{x^2}{5}$=1 | C. | $\frac{x^2}{4}$-$\frac{y^2}{5}$=1(x≤-2) | D. | $\frac{x^2}{4}$-$\frac{y^2}{5}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
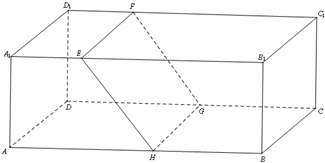 如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.
如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com