
 如图,在圆心角为变量2θ(0<2θ<π)的扇形OAB内作一半径为r的内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,圆P与圆Q相切于C点,圆P和圆Q与半径OA分别切于E,D两点.
如图,在圆心角为变量2θ(0<2θ<π)的扇形OAB内作一半径为r的内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,圆P与圆Q相切于C点,圆P和圆Q与半径OA分别切于E,D两点.分析 (1)由题意得OA=$\frac{1+sinθ}{sinθ}$,QD=$\frac{1-sinθ}{1+sinθ}$r,由QD≥$\frac{OA}{9}$可得sinθ的不等式,解不等式解正弦函数的单调性可得;
(2)可得$\frac{BH}{PE}$=2cosθ(1+sinθ),设f(θ)=cosθ(1+sinθ),θ∈(0,$\frac{π}{2}$),由导数法可得函数的最值,可得结论.
解答 解:(1)由题意得OP=$\frac{PE}{sinθ}$=$\frac{r}{sinθ}$,
又OP+PE=OA,∴$\frac{r}{sinθ}$+r=OA,∴OA=$\frac{1+sinθ}{sinθ}$r,
又OQ=$\frac{QD}{sinθ}$且OP=OQ+CQ+PC,∴$\frac{r}{sinθ}$=$\frac{QD}{sinθ}$+QD+r,
∴QD=$\frac{1-sinθ}{1+sinθ}$r
则当圆Q的半径不小于$\frac{OA}{9}$,即QD≥$\frac{OA}{9}$也即$\frac{1-sinθ}{1+sinθ}$r≥$\frac{1+sinθ}{9sinθ}$r,
整理得10sin2θ-7sinθ+1≤0,即$\frac{1}{5}$≤sinθ≤$\frac{1}{2}$,
又θ∈(0,$\frac{π}{2}$),y=sinθ在θ∈(0,$\frac{π}{2}$)单调增,
故θ的最大值为$\frac{π}{6}$;
(2)∵BH=OBsin2θ=sin2θ×$\frac{1+sinθ}{sinθ}$r=2cosθ(1+sinθ)r,
∴$\frac{BH}{PE}$=2cosθ(1+sinθ),设f(θ)=cosθ(1+sinθ),θ∈(0,$\frac{π}{2}$),
则f′(θ)=-sinθ(1+sinθ)+cos2θ=-2sin2θ-sinθ+1
令f′(θ)>0可解得-1<sinθ<$\frac{1}{2}$,可得θ∈(0,$\frac{π}{6}$),
同理令f′(θ)<0可得θ∈($\frac{π}{6}$,$\frac{π}{2}$),
则当θ∈(0,$\frac{π}{6}$)时,f(θ)为增函数,当θ∈($\frac{π}{6}$,$\frac{π}{2}$)时,f(θ)为减函数,
∴当θ=$\frac{π}{6}$时,$\frac{BH}{PE}$取得最大值,此时OA=$\frac{1+\frac{1}{2}}{\frac{1}{2}}$r=3r,
故“最理想扇形”的面积为$\frac{1}{2}×\frac{π}{6}×O{A}^{2}$=$\frac{π}{12}×(3r)^{2}$=$\frac{3}{4}π{r}^{2}$
点评 本题考查导数和三角函数的综合应用,涉及新定义和导数法判函数的单调性,属难题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{58}{9}$,-6) | B. | (-$\frac{37}{3}$,-9) | C. | (-$\frac{37}{3}$,9) | D. | (-$\frac{37}{3}$,-6) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
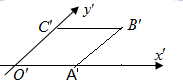 已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )
已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com