
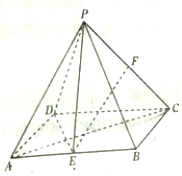
分析 根据面面垂直的判定定理,只要证明DE⊥平面PAC,再证明平面PAC⊥平面PDE.
解答 证明:设AC∩DE=G,由△AEG∽△CDG及E为AB中点得$\frac{AG}{CG}=\frac{AE}{CD}=\frac{1}{2}$,
又因为AB=$\sqrt{2}$,BC=1,所以AC=$\sqrt{3}$,AG=$\frac{1}{3}$AC=$\frac{\sqrt{3}}{3}$.
所以$\frac{AG}{AE}=\frac{AB}{AC}=\frac{\sqrt{2}}{\sqrt{3}}$,
又∠BAC为公共角,所以△GAE∽△BAC.
所以∠AGE=∠ABC=90°,即DE⊥AC.
又DE⊥PA,PA∩AC=A,
所以DE⊥平面PAC.
又DE?平面PDE,
所以平面PAC⊥面PDE.
点评 本题以四棱锥为例,考查了空间的平面与平面垂直的判定,属于中档题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:高中数学 来源: 题型:解答题
 将正偶数列{2n}中的所有项按每一行比上一行多一项的规则排成如图数表:记aij是这个数表的第i行第j列的数.例如a43=18.
将正偶数列{2n}中的所有项按每一行比上一行多一项的规则排成如图数表:记aij是这个数表的第i行第j列的数.例如a43=18.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
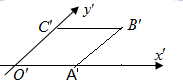 已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )
已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com