
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsin(θ+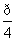 )=
)= a,曲线C2的参数方程为
a,曲线C2的参数方程为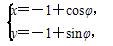 (φ为参数,0≤φ≤π).
(φ为参数,0≤φ≤π).
(1)求C1的直角坐标方程;
(2)当C1与C2有两个不同公共点时,求实数a的取值范围.
科目:高中数学 来源: 题型:
在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝,第二件首饰由6颗珠宝(图中圆圈表示珠宝)构成如图1所示的正六边形,第三件首饰由15颗珠宝构成如图2所示的正六边形,第四件首饰是由28颗珠宝构成如图3所示的正六边形,第五件首饰是由45颗珠宝构成如图4所示的正六边形,以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断前10件首饰所用珠宝总颗数为( )
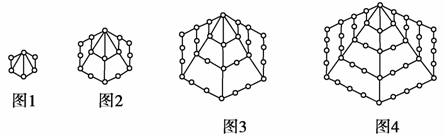
A.190 B.715
C.725 D.385
查看答案和解析>>
科目:高中数学 来源: 题型:
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.曲线C1的参数方程为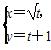 (t为参数),曲线C2的极坐标方程为ρsinθ-ρcosθ=3,则C1与C2的交点在直角坐标系中的坐标为________.
(t为参数),曲线C2的极坐标方程为ρsinθ-ρcosθ=3,则C1与C2的交点在直角坐标系中的坐标为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在直角坐标系xOy中,曲线C1的参数方程为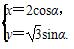 (α为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为ρ(cosθ-sinθ)+1=0,则C1与C2的交点个数为________.
(α为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为ρ(cosθ-sinθ)+1=0,则C1与C2的交点个数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=|x-7|-|x-3|.
(1)作出函数f(x)的图象;
(2)当x<5时,不等式|x-8|-|x-a|>2恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证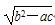 <
<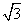 a”“索”的“因”应是( )
a”“索”的“因”应是( )
A.a-b>0 B.a-c>0
C.(a-b)(a-c)>0 D.(a-b)(a-c)<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com