
分析 将一枚硬币连续抛掷5次,正面向上的次数X~B(5,$\frac{1}{2}$),由此能求出正面向上的次数X的分布列.
解答 解:将一枚硬币连续抛掷5次,正面向上的次数X~B(5,$\frac{1}{2}$),
P(X=0)=${C}_{5}^{0}(\frac{1}{2})^{5}$=$\frac{1}{32}$,
P(X=1)=${C}_{5}^{1}(\frac{1}{2})(\frac{1}{2})^{4}$=$\frac{5}{32}$,
P(X=2)=${C}_{5}^{2}(\frac{1}{2})^{2}(\frac{1}{2})^{3}$=$\frac{10}{32}$,
P(X=3)=${C}_{5}^{3}(\frac{1}{2})^{3}(\frac{1}{2})^{2}$=$\frac{10}{32}$,
P(X=4)=${C}_{5}^{4}(\frac{1}{2})^{4}(\frac{1}{2})$=$\frac{5}{32}$,
P(X=5)=${C}_{5}^{5}(\frac{1}{2})^{5}$=$\frac{1}{32}$,
∴正面向上的次数X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{32}$ | $\frac{5}{32}$ | $\frac{10}{32}$ | $\frac{10}{32}$ | $\frac{5}{32}$ | $\frac{1}{32}$ |
点评 本题考查离散型随机变量的分布列的求法,是基础题,解题时要认真审题,注意二项分布的合理运用.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
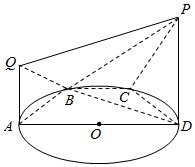 如图,等腰梯形ABCD的底角A等于60°,其外接圆圆心O在边AD上,直角梯形PDAQ垂直于圆O所在平面,∠QAD=∠PDA=90°,且AD=2AQ=4
如图,等腰梯形ABCD的底角A等于60°,其外接圆圆心O在边AD上,直角梯形PDAQ垂直于圆O所在平面,∠QAD=∠PDA=90°,且AD=2AQ=4查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x与y正相关,x与z负相关 | B. | x与y负相关,x与z正相关 | ||
| C. | z与y正相关,x与z正相关 | D. | x与y负相关,x与z负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某构件是由编号1、2、…、k(k∈N*且k≥3)的有限个圆柱自下而上组成的,其中每一个圆柱的高与其底面圆的直径相等,且对于任意两个相邻圆柱,上面圆柱的高是下面圆柱的高的一半,设编号1的圆柱的高为4.
如图,某构件是由编号1、2、…、k(k∈N*且k≥3)的有限个圆柱自下而上组成的,其中每一个圆柱的高与其底面圆的直径相等,且对于任意两个相邻圆柱,上面圆柱的高是下面圆柱的高的一半,设编号1的圆柱的高为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意n∈N*,P(n)是真命题 | |
| B. | 对任意n∈N*,仅有P(2n)是真命题 | |
| C. | 对任意n∈N*,仅有P(2n)和P(2n-1)是真命题 | |
| D. | 对任意n∈N*,P(n)不是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com