
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 $x∈({0,\frac{π}{2}})$,令f(x)=x-sinx,利用导数研究其单调性即可判断出命题p的真假.而$x∈({0,\frac{π}{2}})$,令g(x)=x2-sinx,同理判断出此命题的真假.
解答 解:$x∈({0,\frac{π}{2}})$,令f(x)=x-sinx,则f′(x)=1-cosx>0,∴函数f(x)在$x∈({0,\frac{π}{2}})$上单调递增,则f(x)>f(0)=0,因此命题p是真命题.
而$x∈({0,\frac{π}{2}})$,令g(x)=x2-sinx,则g′(x)=2x-cosx,${g}^{′}(0){g}^{′}(\frac{π}{2})$=-1×π<0,∴g′(x)=0有解,因此函数g(x)存在极值点,设为x0,则2x0=cosx0.g(x0)=${x}_{0}^{2}$-sinx0=$\frac{co{s}^{2}{x}_{0}}{4}$-sinx0=$\frac{-si{n}^{2}{x}_{0}-4sin{x}_{0}+1}{4}$=$\frac{-(sin{x}_{0}+2)^{2}+5}{4}$∈$(-1,\frac{1}{4})$,因此命题q不一定成立.
∴p是q的必要不充分条件.
故选:B.
点评 本题考查了利用导数研究函数的单调性极值与最值、三角函数求值、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | $({-\frac{1}{3},1}]$ | C. | [1,+∞) | D. | $({-∞,\frac{1}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
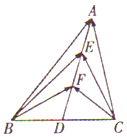 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )| A. | 4 | B. | 8 | C. | $\frac{7}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com