
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
分析 先将直线的极坐标方程化为直角坐标方程,曲线C的参数方程化为普通方程,然后利用代数法或几何法解答.
解答 方法一:代数法
直线l:ρcosθ-ρsinθ+1=0⇒x-y+1=0,
曲线C:$\left\{\begin{array}{l}{x=\sqrt{2}cosθ}\\{y=\sqrt{2}sinθ}\end{array}\right.$⇒x2+y2=2,
联立,$\left\{\begin{array}{l}{y=x+1}\\{{x}^{2}+{y}^{2}=2}\end{array}\right.$,得x2+(x+1)2-2=0,
即2x2+2x-1=0,设A(x1,y1),B(x2,y2),
由韦达定理,$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=-1}\\{{x}_{1}{x}_{2}=-\frac{1}{2}}\end{array}\right.$,
所以$|AB|=\sqrt{1+{k}^{2}}|{x}_{1}-{x}_{2}|$=$\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{6}$,选D.
方法二:几何法
直线l:ρcosθ-ρsinθ+1=0⇒x-y+1=0,
曲线C:$\left\{\begin{array}{l}{x=\sqrt{2}cosθ}\\{y=\sqrt{2}sinθ}\end{array}\right.$⇒x2+y2=2,
圆心(0,0)到直线x-y+1=0的距离$d=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,
半径$r=\sqrt{2}$,所以$|AB|=2\sqrt{{r}^{2}-{d}^{2}}=\sqrt{6}$,选D.
注:当然此题也可以直接求出A,B两点的坐标,然后利用两点之间的距离公式求解.
点评 极坐标和参数方程问题一般化为熟悉的直角坐标问题,所以转化是解决此类问题的关键.


科目:高中数学 来源: 题型:填空题
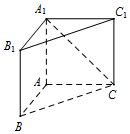 如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=$\sqrt{2}$,则异面直线A1C与B1C1所成的角为$\frac{π}{3}$..
如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=$\sqrt{2}$,则异面直线A1C与B1C1所成的角为$\frac{π}{3}$..查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
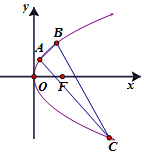 给定直线l:y=2x-16,抛物线G:y2=ax(a>0)
给定直线l:y=2x-16,抛物线G:y2=ax(a>0)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com