考点:点、线、面间的距离计算,平行公理
专题:空间位置关系与距离
分析:(1)连接DM并延长交D
1A
1延长线于E,连接NE即是所求直线l;
(2)容易求得
A1P=a,所以B
1P=
a,又BB
1=a,所以在Rt△BB
1P中,可求出BP;
(3)求A到l的距离,所以想着找过a,与l垂直的线段,所以过A
1作l的垂线,垂足为F,连接AF,容易说明AF⊥l,所以根据一些边的长度求AF长度即可.
解答:
解:(1)如图,连接DM,并延长交DA
1延长线于E,连接NE,则NE即为所找直线l;
(2)根据已知条件知:MA
1∥DD
1,且
MA1=DD1,∴A
1为ED
1的中点;
A1P=D1N=a,∴
B1P=a,BB
1=a,∴PB=
=;
(3)过A
1作A
1F⊥l,垂足为F,连接AF,∵AA
1⊥平面ED
1N,EN?平面ED
1N,∴AA
1⊥EN即EN⊥AA
1,又EN⊥A
1F,AA
1∩A
1F=A
1,∴EN⊥平面AA
1F,AF?平面AA
1F,∴EN⊥AF,∴求A到l的距离,求AF的长度即可;
EP=
EN==,∴在Rt△EA
1P中,A
1E•A
1P=EP•A
1F,∴
a•=•A1F,∴
A1F=;
∴在Rt△AA
1P中,AA
1,AP=
=,即A到l的距离为:
.
点评:三角形的中位线,直角三角形中边的关系,线面垂直的性质,线面垂直的判定定理.

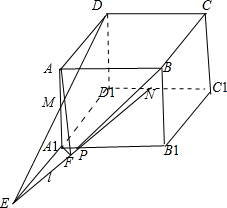
 在棱长为a的正方体ABCD-A1B1C1D1中,M、N分别为A1A、D1C1的中点,过D、M、N三点的平面与正方体的下底面A1B1C1D1相交与直线l.
在棱长为a的正方体ABCD-A1B1C1D1中,M、N分别为A1A、D1C1的中点,过D、M、N三点的平面与正方体的下底面A1B1C1D1相交与直线l. (2)根据已知条件知:MA1∥DD1,且MA1=
(2)根据已知条件知:MA1∥DD1,且MA1=

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案