
| m |
| x |
| 2 |
| n |
| 3 |
| x |
| 2 |
| x |
| 2 |
| m |
| n |
| 1 |
| 2 |
| π |
| 2 |
| ||
| 3 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| ||
| 3 |
| 3 |
| ||
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| ||
| 3 |
| π |
| 6 |
| ||
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| ||
| 6 |
| 3 |
| b2+c2-a2 |
| 2bc |
| 3 |
| 3 |
| ||
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| n+1 |
| n |
| Sn |
| n3+3n2 |
| 5 |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
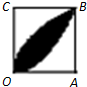 在正方形OABC框格内有一块花纹(如图所示),花纹刚好过点O,B,经研究发现花纹边界是函数y=x2与y=
在正方形OABC框格内有一块花纹(如图所示),花纹刚好过点O,B,经研究发现花纹边界是函数y=x2与y=| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某市政府为了了解居民的生活用电情况,以使全市在用电高峰月份的居民生活不受影响,决定制定一个合理的月均用电标准.为了确定一个较为合理的标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,其样本统计结果如下图表:
某市政府为了了解居民的生活用电情况,以使全市在用电高峰月份的居民生活不受影响,决定制定一个合理的月均用电标准.为了确定一个较为合理的标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,其样本统计结果如下图表:| 分组 | 频数 | 频率 |
| [0,10] | 0.05 | |
| [10,20] | 0.20 | |
| [20,30] | 35 | |
| [30,40] | a | |
| [40,50] | 0.15 | |
| [50,60] | 5 | |
| 合计 | N | 1 |
| 1 |
| 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com