
分析 由已知利用递推公式an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}{-S}_{n-1},n≥2,n∈N*}\end{array}\right.$可得an,代入分别可求数列bn的首项b1,公比q,从而可求bn.
解答 解:当n=1时,a1=S1=2;当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2,
上式对n=1也成立,
故{an}的通项公式为an=4n-2.即{an}是a1=2,公差d=4的等差数列.
设{bn}的公比为q,
由a1=b1,b2(a2-a1)=b1,
可得b1qd=b1,又d=4,
可得q=$\frac{1}{4}$.
故bn=b1qn-1=2×$\frac{1}{{4}^{n-1}}$,即{bn}的通项公式为bn=$\frac{2}{{4}^{n-1}}$,n∈N*.
点评 当已知条件中含有sn时,一般会用结论an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}{-S}_{n-1},n≥2,n∈N*}\end{array}\right.$来求通项,一般有两种类型:①所给的Sn=f(n),则利用此结论可直接求得n>1时数列{an}的通项,但要注意检验n=1是否适合②所给的Sn是含有an的关系式时,则利用此结论得到的是一个关于an的递推关系,再用求通项的方法进行求解.


科目:高中数学 来源: 题型:选择题
| A. | π+1 | B. | π+2 | C. | 2π | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 观察如图三角形数表,假设第n行第二个数为an(n≥2,n∈N*)
观察如图三角形数表,假设第n行第二个数为an(n≥2,n∈N*)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
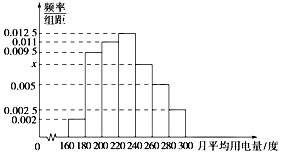 节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 培养液处理 | 未处理 | 合计 | |
| 青花病 | 30 | 224 | 254 |
| 无青花病 | 24 | 1355 | 1379 |
| 合计 | 54 | 1579 | 1633 |
| P(K2≥k) | 0.05 | 0.01 | 0.005 | 0.001 |
| k | 3.841 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com