
分析 (Ⅰ)运用代入法,结合等差数列的定义和通项公式,可得所求;
(Ⅱ)求得bn=$\frac{{3}^{n}}{{{a}_{n}}^{2}}$,运用错位相减法,可得前n项和Sn;
(Ⅲ)求得cn=an2•an+12,运用裂项相消求和,可得Tn,且Tn<$\frac{1}{4}$,由不等式恒成立思想可得不等式,解不等式,即可得到所求.
解答 解:(Ⅰ)-$\frac{1}{{a}_{n+1}}$=f(an)=-$\sqrt{4+\frac{1}{{{a}_{n}}^{2}}}$且an>0,
∴$\frac{1}{{{a}_{n+1}}^{2}}$-$\frac{1}{{{a}_{n}}^{2}}$=4,
∴数列{$\frac{1}{{{a}_{n}}^{2}}$}是等差数列,
首项$\frac{1}{{{a}_{1}}^{2}}$=1,公差d=4,
∴$\frac{1}{{{a}_{n}}^{2}}$=1+4(n-1),
∴an2=$\frac{1}{4n-3}$,
∵an>0,
∴an=$\sqrt{\frac{1}{4n-3}}$;
(Ⅱ)bn=$\frac{{3}^{n}}{{{a}_{n}}^{2}}$=(4n-3)•3n,
Sn=1•3+5•32+…+(4n-3)•3n,
3Sn=1•32+5•33+…+(4n-3)•3n+1,
两式相减可得-2Sn=3+4(32+33+…+3n)-(4n-3)•3n+1,
=3+4•$\frac{9(1-{3}^{n-1})}{1-3}$-(4n-3)•3n+1,=-15-(4n-3))•3n+1,
则有Sn=$\frac{15+(4n-5)•{3}^{n+1}}{2}$.
(Ⅲ)cn=an2•an+12=$\frac{1}{(4n-3)(4n+1)}$=$\frac{1}{4}$($\frac{1}{4n-3}$-$\frac{1}{4n+1}$),
Tn=c1+c2+…+cn=$\frac{1}{4}$[(1-$\frac{1}{5}$)+($\frac{1}{5}$-$\frac{1}{9}$)+…+($\frac{1}{4n-3}$-$\frac{1}{4n+1}$)]
=$\frac{1}{4}$(1-$\frac{1}{4n+1}$)<$\frac{1}{4}$,
由于Tn<t2-t-$\frac{1}{2}$对任意的n∈N*恒成立,
则t2-t-$\frac{1}{2}$≥$\frac{1}{4}$,解得t≥$\frac{3}{2}$或t≤-$\frac{1}{2}$,
即为t的范围为(-∞,-$\frac{1}{2}$]∪[$\frac{3}{2}$,+∞).
点评 本题主要考查了利用数列的递推公式求解数列的通项公式,解(Ⅰ)题的关键是构造等差的形式,裂项求和和错位相减法是数列求和中的重要方法,要注意掌握.


科目:高中数学 来源: 题型:解答题
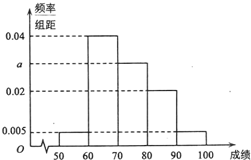 某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -1 | C. | -1或$\frac{3}{2}$ | D. | 1或-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为$\frac{5}{9}$.
在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为$\frac{5}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com