
分析 (1)由题可知生产100件这样的产品单价为50万元,所以把x=100,P=50代入到p2=$\frac{k}{x}$中求出k的值确定出P的解析式,然后根据总利润=总销售额-总成本得出L(x)即可;
(2)令L′(x)=0求出x的值,此时总利润最大,最大利润为L(25).
解答 解:(1)由题意有502=$\frac{k}{100}$,解得k=25×104,∴P=$\sqrt{\frac{25{×10}^{4}}{x}}$=$\frac{500}{\sqrt{x}}$,
∴总利润L(x)=x•$\frac{500}{\sqrt{x}}$-1200-$\frac{{2x}^{3}}{75}$=-$\frac{2}{75}$x3+500$\sqrt{x}$-1200(x>0);
(2)由(1)得L′(x)=-$\frac{2}{25}$x2+$\frac{250}{\sqrt{x}}$,令L′(x)=0⇒$\frac{250}{\sqrt{x}}$=$\frac{2}{25}$x2,
令t=$\sqrt{x}$,得 $\frac{250}{t}$=$\frac{2}{25}$t4⇒t5=125×25=55,∴t=5,于是x=t2=25,
则x=25,所以当产量定为25时,总利润最大.
这时L(25)≈-416.7+2500-1200≈883.
答:产量x定为25件时总利润L(x)最大,约为883万元.
点评 考查学生根据实际问题选择函数关系的能力,及利用导数求函数最值的方法的能力.


科目:高中数学 来源: 题型:解答题
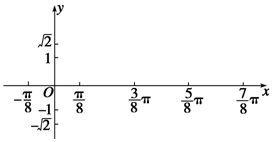 已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(cosα)>f(cosβ) | B. | f(sinα)>f(sinβ) | C. | f(sinα)<f(cosβ) | D. | f(sinα)>f(cosβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{b_1}{a_1}•\frac{b_2}{a_2}=-1$ | B. | a1a2+b1b2=0 | ||
| C. | $\frac{b_1}{a_1}=\frac{b_2}{a_2}$ | D. | a1b2=a2b1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com