
分析 (1)a1=1,an+1=$\frac{{n}^{2}{a}_{n}+{{a}_{n}}^{2}}{{{a}_{n}}^{2}+2{a}_{n}-n}+1$,n∈N*.分别令n=1,2,3,可得a2=2,a3=3,a4=4,猜想通项公式an=n.用数学归纳法证明即可.
(2)利用(1)的结论an=n,利用数学归纳法证明即可.
解答 (1)解:a1=1,an+1=$\frac{{n}^{2}{a}_{n}+{{a}_{n}}^{2}}{{{a}_{n}}^{2}+2{a}_{n}-n}+1$,n∈N*.分别令n=1,2,3,可得a2=2,a3=3,a4=4,
猜想通项公式an=n.
用数学归纳法证明猜想.
(i)当n=1时,a1=1成立.
(ii)假设当n=k∈N*时,ak=k成立.
则当n=k+1时,ak+1=$\frac{{k}^{2}×k+{k}^{2}}{{k}^{2}+2k-k}$+1=k+1,
∴当n=k+1时,ak+1=k+1,等式成立.
综上可得:等式an=n对于?n∈N*都成立.
∴an=n.
(2)证明:用数学归纳法证明.
(i)当n=1时,左边=$\sqrt{{a}_{1}{a}_{2}}$=$\sqrt{2}$,右边=$\frac{1}{2}×(1+1)^{2}$=2,∴左边<右边.
(ii)假设当n=k∈N*时,不等式$\sqrt{{{a}_{1}a}_{2}}$+$\sqrt{{a}_{2}{a}_{3}}$+…+$\sqrt{{a}_{k}{a}_{k+1}}$<$\frac{1}{2}$(ak+1)2,k∈N*成立.
则当n=k+1时,左边=$\sqrt{{{a}_{1}a}_{2}}$+$\sqrt{{a}_{2}{a}_{3}}$+…+$\sqrt{{a}_{k}{a}_{k+1}}$+$\sqrt{{a}_{k+1}{a}_{k+2}}$<$\frac{1}{2}$(ak+1)2+$\sqrt{{a}_{k+1}{a}_{k+2}}$=$\frac{1}{2}(k+1)^{2}$+$\sqrt{(k+1)(k+2)}$<$\frac{1}{2}(k+1)^{2}$+$\frac{(k+1)+(k+2)}{2}$=$\frac{1}{2}$(k+2)2.
∴当n=k+1时,不等式成立.
综上可得:不等式对于?n∈N*都成立.
点评 本题考查了递推式的应用、数学归纳法、不等式的性质,考查了猜想与归纳推理能力与计算能力,属于中档题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
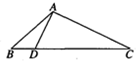 如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3,求BD的长.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3,求BD的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 46 | B. | 44 | C. | 33 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中正确的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中正确的是( ) | A. | ①② | B. | ①②③ | C. | ②③ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com