
分析 (1))(用综合法),作差证明即可;
(2)(用反证法)研究的三个方程至少有一个有实根,此类题求解时通常转化为求其对立面,研究三个方程都没有实根时实数a的取值集合,其补集即是所求的实数a的取值范围.
解答 证明(1):(用综合法)$\frac{a}{{\sqrt{b}}}+\frac{b}{{\sqrt{a}}}-(\sqrt{a}+\sqrt{b})=\frac{a}{{\sqrt{b}}}-\sqrt{b}+\frac{b}{{\sqrt{a}}}-\sqrt{a}=\frac{a-b}{{\sqrt{b}}}+\frac{b-a}{{\sqrt{a}}}$,
=$(a-b)(\frac{1}{{\sqrt{b}}}-\frac{1}{{\sqrt{a}}})=\frac{{{{(\sqrt{a}-\sqrt{b})}^2}(\sqrt{a}+\sqrt{b})}}{{\sqrt{ab}}}$.
∵a>0,b>0,
∴$\frac{{{{(\sqrt{a}-\sqrt{b})}^2}(\sqrt{a}+\sqrt{b})}}{{\sqrt{ab}}}≥0$,
∴$\frac{a}{{\sqrt{b}}}+\frac{b}{{\sqrt{a}}}≥\sqrt{a}+\sqrt{b}$.
(2):假设没有一个方程有实数根,则:
16a2-4(3-4a)<0,①
(a-1)2-4a2<0,②
4a2+8a<0,③,
由①②③解得:-$\frac{3}{2}$<a<-1,
故三个方程至少有一个方程有实根的a的取值范围是:{a|a≥-1或a≤-$\frac{3}{2}$}.
点评 本题考查了作差法比较大小以及反证法,考查了学生的转化能力和运算能力,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<0或a>1 | B. | a≤0或a≥1 | C. | 0≤a≤1 | D. | 0<a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}$ | B. | -1 | C. | $\frac{5}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
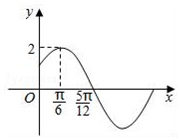 已知函数f(x)=Asin(ωx+φ)
已知函数f(x)=Asin(ωx+φ)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{9}{2}$] | B. | (-∞,1] | C. | (-∞,9] | D. | (-∞,8] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com