
分析 令g(x)=$\frac{f(x)}{x}$,得到g(x)在(0,+∞)递减,通过${log}_{2}^{5}$>20.2>0.22,从而得出答案
解答 解:令g(x)=$\frac{f(x)}{x}$,则g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,
∵x>0时,xf′(x)-f(x)<0,
∴g(x)在(0,+∞)递减,
又${log}_{2}^{5}$>${log}_{2}^{4}$=2,1<20.2<2,0.22=0.04,
∴${log}_{2}^{5}$>20.2>0.22,
∴g(${log}_{2}^{5}$)<g(20.2)<g(0.22),
∴c<a<b,
故答案为:c<a<b.
点评 本题考查了函数的单调性问题,考查了导数的应用,考查了指数,对数的性质,是一道中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
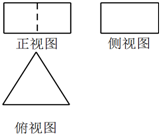 如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$.
如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
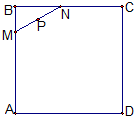 正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )| A. | $\frac{7}{8}$ | B. | $\frac{π}{16}$ | C. | $1-\frac{π}{16}$ | D. | $\frac{3}{4}+\frac{π}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com