练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．方程lg（2x2+x）=0的解x为-1或$\frac{1}{2}$．

    分析 由lg（2x2+x）=0，得2x2+x=1，由此能求出结果．

    解答 解：∵lg（2x2+x）=0，
    ∴2x2+x=1，
    解得x=-1或x=$\frac{1}{2}$．
    故答案为：-1或$\frac{1}{2}$．

    点评 本题考查对数方程的解的求法，是基础题，解题时要认真审题，注意对数性质、运算法则的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．下列函数中，既是偶函数又在区间 （0，+∞）上单调递减的是（　　）
    A．y=$\frac{1}{x}$B．y=e-xC．y=-x2+1D．y═lg|x|

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知sin（30°+α）=$\frac{4}{5}$，60°＜α＜150°，则cosα=$\frac{4-3\sqrt{3}}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．如图，在△OBC中，点A是BC的中点，$\overrightarrow{OD}$=2$\overrightarrow{DB}$，DC和OA交于点E，则AO与OE的比值为（　　）
    A．$\frac{6}{5}$B．$\frac{3}{2}$C．$\frac{5}{4}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

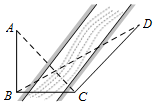    14．如图，某人为测量河对岸塔AB的高，先在塔底B的正东方向上的河岸上选一点C，在点C处测得点A的仰角为45°，并在点C北偏东15°方向的河岸上选定一点D，测得CD的距离为20米，∠BDC=30°，则塔AB的高是（　　）
    A．10米B．$10\sqrt{2}$米C．$10\sqrt{3}$米D．$20\sqrt{3}$米

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

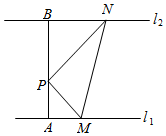    7．如图，P是两条平行直线l1，l2之间的一个定点，且点P到l1，l2的距离分别为PA=1，PB=$\sqrt{3}$，设△PMN的另两个顶点M，N分别在l1，l2上运动，设∠MPN=α，∠PMN=β，∠PNM=γ，且满足sinβ+sinγ=sinα（cosβ+cosγ）．
    （Ⅰ）求α；
    （Ⅱ）求$\frac{1}{PM}$+$\frac{\sqrt{3}}{PN}$的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知△ABC的面积为$\frac{\sqrt{3}}{2}$，$\overrightarrow{AB}$$•\overrightarrow{AC}$=-3，则A=$\frac{5π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=xlnx+ax（a∈R）．
    （1）若函数f（x）在区间[e，e2]上为减函数，求a的取值范围；
    （2）若对任意x∈（1，+∞），f（x）＞k（x-1）+ax-x恒成立，求正整数k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．在圆x2+my2-2x+4y=0上存在两个点以直线nx+4y=0为对称轴，则m+n=9．

    查看答案和解析>>

    同步练习册答案