
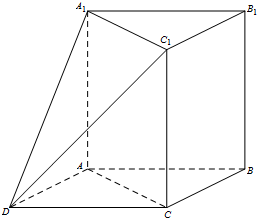
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1. 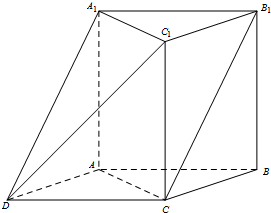 (本小题共13分)
(本小题共13分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
| 3 |
A、若α≠
| ||||
B、若α=
| ||||
C、若tanα≠
| ||||
D、若tanα=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(-∞,1] |
| B、(-∞,-8] |
| C、[1,+∞) |
| D、[-8,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
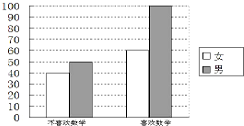 为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.| 男 | 女 | 合计 | |
| 喜欢数学课程 | |||
| 不喜欢数学课程 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| x |
| 2 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com